Question

【题目】已知直线l1过点A(0,1)，l2过点B(5,0)，如果l1∥l2，且l1与l2间的距离为5，求l1、l2的方程．

Answer 1

【答案】见解析

【解析】当l1、l2的斜率存在时，∵l1∥l2，∴可设两直线的斜率为k.

由斜截式得l1的方程为y＝kx＋1，即kx－y＋1＝0.由点斜式得l2的方程为y＝k(x－5)，即kx－y－5k＝0.由两平行线间的距离公式得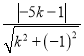＝5，解得k＝，∴l1的方程为12x－5y＋5＝0，l2的方程为12x－5y－60＝0.

若l1、l2的斜率不存在，则l1的方程为x＝0，l2的方程为x＝5，它们之间的距离为5，同样满足条件．

则满足条件的直线方程为l1：12x－5y＋5＝0，l2：12x－5y－60＝0或l1：x＝0，l2：x＝5.