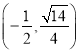题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调递减区间;
的单调递减区间;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值
的最小值
【答案】(1)![]() ;(2)2
;(2)2
【解析】试题分析:
(1)由![]() 可求得
可求得![]() ,求导后令
,求导后令![]() 解不等式可得单调递减区间.(2)构造函数
解不等式可得单调递减区间.(2)构造函数![]() ,则问题等价于
,则问题等价于![]() 在
在![]() 上恒成立.当
上恒成立.当![]() 时,求导可得
时,求导可得![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,故不满足题意.当
,故不满足题意.当![]() 时,可得
时,可得![]() 的最大值为
的最大值为![]() ,因为
,因为![]() 单调递减,且
单调递减,且![]() ,
, ![]() ,所以当
,所以当![]() 时,
时, ![]() ,从而可得整数
,从而可得整数![]() 的最小值为2.
的最小值为2.
试题解析:
(1)因为![]() ,
,
所以![]() ,
,
故![]() ,
,
所以![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() 的单调减区间为
的单调减区间为![]() .
.
(2)令![]() ,
, ![]() ,
,
由题意可得![]() 在
在![]() 上恒成立.
上恒成立.
又![]() .
.
①当![]() 时,则
时,则![]() .
.
所以![]() 在
在![]() 上单调递增,
上单调递增,
又因为![]() ,
,
所以关于![]() 的不等式
的不等式![]() 不能恒成立.
不能恒成立.
②当![]() 时,
时, 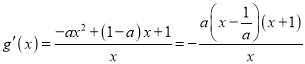 ,
,
令![]() ,得
,得![]() .
.
所以当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递减.
单调递减.
故当![]() 时,函数
时,函数![]() 取得极大值,也为最大值,且最大值为
取得极大值,也为最大值,且最大值为![]() .
.
令![]() ,
,
则![]() 在
在![]() 上单调递减,
上单调递减,
因为![]() ,
, ![]() .
.
所以当![]() 时,
时, ![]() ,
,
所以整数![]() 的最小值为2.
的最小值为2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两人进行射击比赛,各射击![]() 局,每局射击
局,每局射击![]() 次,射击命中目标得
次,射击命中目标得![]() 分,未命中目标得
分,未命中目标得![]() 分,两人
分,两人![]() 局的得分情况如下:
局的得分情况如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(Ⅰ)若从甲的![]() 局比赛中,随机选取
局比赛中,随机选取![]() 局,求这
局,求这![]() 局的得分恰好相等的概率.
局的得分恰好相等的概率.
(Ⅱ)如果![]() ,从甲、乙两人的
,从甲、乙两人的![]() 局比赛中随机各选取
局比赛中随机各选取![]() 局,记这
局,记这![]() 局的得分和为
局的得分和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(Ⅲ)在![]() 局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)