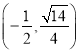题目内容
【题目】设等差数列![]() 的前
的前![]() 项和
项和![]() ,且
,且![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若不等式![]() 对所有的正整数
对所有的正整数![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(1)根据等差数列通项公式以及求和公式将条件化为关于首项与公差的方程组,解得![]() .(2)先化简不等式:
.(2)先化简不等式: ![]() ,再分奇偶讨论:当
,再分奇偶讨论:当![]() 为奇数时,
为奇数时, ![]() ; 当
; 当![]() 为偶数时,
为偶数时, ![]() ,最后根据基本不等式以及数列单调性确定实数
,最后根据基本不等式以及数列单调性确定实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)设公差为![]() ,则
,则![]() ,∴
,∴![]() .
.
∴![]() 的通项公式为
的通项公式为![]() .
.
(Ⅱ)![]() ,
, ![]() ,
, ![]() ;
;
则原不等式等价于![]() 对所有的正整数
对所有的正整数![]() 都成立.
都成立.
∴当![]() 为奇数时,
为奇数时, ![]() ; 当
; 当![]() 为偶数时,
为偶数时, ![]() 恒成立
恒成立
又∵![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以当![]() 为奇数时,
为奇数时, ![]() 的最小值为7,
的最小值为7,
当![]() 为偶数时,
为偶数时, ![]() 时,
时, ![]() 的最小值为
的最小值为![]() ,
,
∴不等式对所有的正整数![]() 都成立时,实数
都成立时,实数![]() 的取值范是
的取值范是![]()

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目