题目内容
【题目】
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.
【答案】(1)![]() ;(2)
;(2)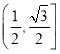 .
.
【解析】
试题(1)要求解,已知条件中有角有边,一般情况下我们可以利用正弦定理把边化为角的关系,本题acosC+ccosA=2bcosA,由正弦定理可化为![]() ,于是有
,于是有![]() ,即
,即![]() ,而
,而![]() ,于是
,于是![]() ,
,![]() ;(2)由(1)
;(2)由(1)![]() ,且
,且![]() ,
,![]() ,由两角和与差的正弦公式可转化为
,由两角和与差的正弦公式可转化为![]() ,再由正弦函数的性质可得取值范围.
,再由正弦函数的性质可得取值范围.
试题解析:(1)因为acosC+ccosA=2bcosA,所以sinAcosC+sinCcosA=2sinBcosA,
即sin(A+C)=2sinBcosA.
因为A+B+C=π,所以sin(A+C)=sinB.
从而sinB=2sinBcosA.
因为sinB≠0,所以![]()
因为0<A<π,所以![]()
(2)![]()
因为![]() ,所以
,所以![]() .
.
所以sinB+sinC的取值范围为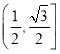 .
.

练习册系列答案
相关题目