题目内容
13.高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数x与答题正确率y%的关系,对某校高三某班学生进行了关注统计,得到如下数据:| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
(Ⅱ)若用$\frac{y_i}{{{x_i}+3}}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$,$\hat a=\bar y-\hat b\bar x$.
样本数据x1,x2,…,xn的标准差为:s=$\sqrt{\frac{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}{n}}$.
分析 (Ⅰ)利用已知条件求出样本中心,回归直线方程的几何量,即可求y关于x的线性回归方程,然后预测答题正确率是100%的强化训练次数;
(Ⅱ)求出这四组数据的“强化均值”分别是5,6,8,9,求解方差,判断结果即可.
解答 解:(Ⅰ)由所给数据计算得$\overline{x}$=$\frac{1+2+3+4}{4}$=2.5,$\overline{y}$=$\frac{20+30+50+60}{4}=40$,
$\sum _{i=1}^{4}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=70,$\sum _{i=1}^{4}({x}_{i}-\overline{x})^{2}=5$,
$\widehat{b}=\frac{\sum _{i=1}^{4}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum _{i=1}^{4}{({x}_{i}-\overline{x})}^{2}}=14$,$\widehat{a}=y-\widehat{b}\overline{x}$=5,
所求回归方程是$\hat{y}=14x+5$,
由100=14x+5,得x=6.79,…(6分)
预测答题正确率是100%的测强化训练次数为7次;
(Ⅱ)经计算知,这四组数据的“强化均值”分别是5,6,8,9,
平均数是7,“强化均值”的标准差是
s=$\sqrt{\frac{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}{n}}$=$\sqrt{\frac{(5-7)^{2}+({6-7)}^{2}+(8-7)^{2}+(9-7)^{2}}{4}}$=$\sqrt{2.5}<2$,
这个班的强化训练有效.…(12分)
点评 本题考查回归直线方程的求法,方差的求法,考查计算能力.

| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
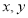 满足条件
满足条件 ,且
,且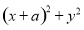 的最小值为6,
的最小值为6,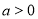 ,则
,则 _____________.
_____________. 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且BN=$\frac{1}{3}$BC 如图,在三棱锥A-BCD中,△ACD与△BCD都是边长为2的正三角形,且平面ACD⊥平面BCD,则该三棱锥外接球的表面积为$\frac{20}{3}π$.
如图,在三棱锥A-BCD中,△ACD与△BCD都是边长为2的正三角形,且平面ACD⊥平面BCD,则该三棱锥外接球的表面积为$\frac{20}{3}π$.