题目内容
设函数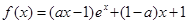 .
.
(Ⅰ)证明:当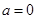 ,
,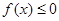 ;
;
(Ⅱ)设当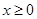 时,
时,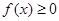 ,求
,求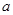 的取值范围.
的取值范围.
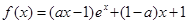 .
. (Ⅰ)证明:当
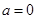 ,
,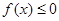 ;
;(Ⅱ)设当
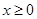 时,
时,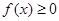 ,求
,求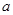 的取值范围.
的取值范围. (Ⅰ)详见解析;(Ⅱ) 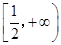 .
.
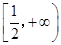 .
.试题分析:(Ⅰ)当
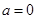 时,求导数
时,求导数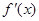 ,令
,令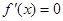 ,
,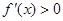 ,
,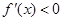 求函数
求函数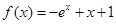 的单调区间与极值,再求最大值
的单调区间与极值,再求最大值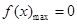 ,从而判断,当
,从而判断,当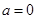 时,
时,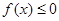 成立;(Ⅱ)由
成立;(Ⅱ)由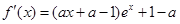 ,注意到
,注意到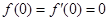 .再求
.再求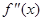 ,对实数
,对实数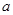 分三种情况讨论,①
分三种情况讨论,①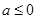 ,②
,②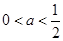 ,③
,③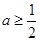 ,分别求出当
,分别求出当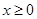 时,分别通过函数
时,分别通过函数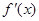 单调性,判断函数
单调性,判断函数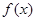 的单调性,从而求得
的单调性,从而求得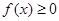 的
的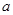 的取值范围,再求并集.
的取值范围,再求并集.试题解析:(Ⅰ)当
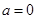 时,
时,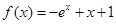 ,则
,则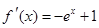
令
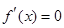 ,得
,得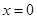 ,当
,当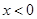 时,
时,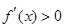 ,所以
,所以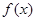 在
在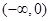 为增函数;
为增函数;当
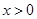 时,
时,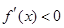 ,所以
,所以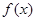 在
在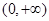 为减函数.
为减函数.所以,
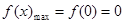 .
.即当
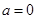 时,
时,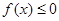 成立. 4分
成立. 4分(Ⅱ)由
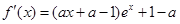 ,注意到
,注意到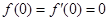 .
.设
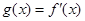 ,则
,则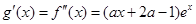 .
. (ⅰ)当
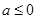 ,
,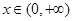 时,
时,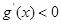 ,因此
,因此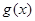 在
在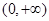 为减函数,
为减函数,即
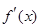 在
在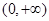 为减函数,
为减函数,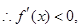 所以
所以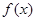 在
在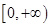 为减函数,
为减函数,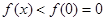 与已知矛盾.
与已知矛盾. (ⅱ)当
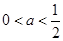 时,当
时,当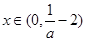 时,
时,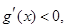
则
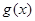 在
在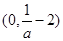 为减函数,此时
为减函数,此时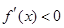 得
得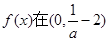 为减函数,
为减函数,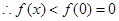 与已知矛盾.
与已知矛盾. (ⅲ)当
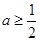 时,当
时,当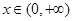 时,
时,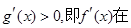
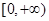 为增函数.
为增函数. 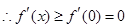 ,所以
,所以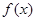 在
在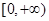 为增函数,
为增函数, 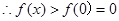 不等式成立.
不等式成立. 综上所述 ,
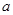 的取值范围是
的取值范围是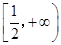

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
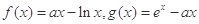 ,其中a为正实数.
,其中a为正实数.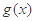 的极值点,讨论函数
的极值点,讨论函数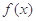 的单调性;
的单调性;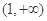 上无最小值,且
上无最小值,且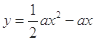 在
在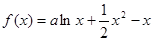
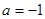 时,求函数
时,求函数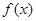 的单调区间;
的单调区间;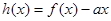 ,对定义域内任意x,均有
,对定义域内任意x,均有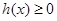 恒成立,求实数a的取值范围?
恒成立,求实数a的取值范围?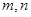 ,
,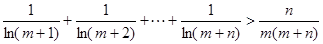 恒成立。
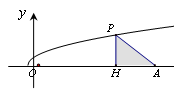
恒成立。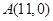 ,直线
,直线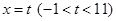 与函数
与函数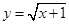 的图象交于点
的图象交于点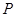 ,与
,与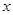 轴交于点
轴交于点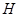 ,记
,记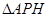 的面积为
的面积为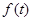 .
.
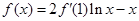 ,则
,则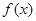 的极大值为 .
的极大值为 .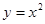 在
在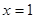 处的切线与两坐标轴围成三角形区域为
处的切线与两坐标轴围成三角形区域为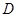 (包含三角形内部与边界).若点
(包含三角形内部与边界).若点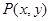 是区域
是区域 的取值范围是__________.
的取值范围是__________.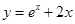 在点
在点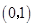 处的切线方程为
处的切线方程为 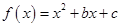 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数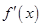 的图象是( )
的图象是( )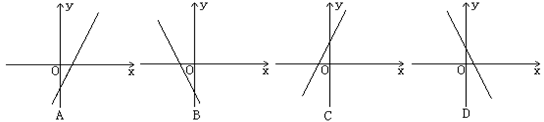
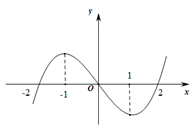
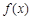 的图像如图所示,则不等式
的图像如图所示,则不等式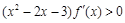 的解集为( )
的解集为( )