题目内容
如图是 函数
函数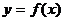
 的导函数
的导函数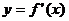 的图象,给出下列命题:
的图象,给出下列命题:
①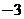 是函数
是函数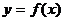 的极值点;
的极值点;
②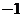 是函数
是函数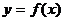 的最小值点;
的最小值点;
③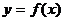 在
在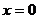 处切线的斜率小于零;
处切线的斜率小于零;
④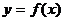 在区间
在区间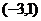 上单调递增。
上单调递增。
则正确命题的序号是 。
 函数
函数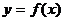
 的导函数
的导函数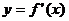 的图象,给出下列命题:
的图象,给出下列命题:①
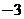 是函数
是函数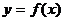 的极值点;
的极值点;②
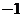 是函数
是函数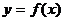 的最小值点;
的最小值点;③
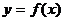 在
在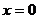 处切线的斜率小于零;
处切线的斜率小于零;④
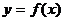 在区间
在区间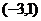 上单调递增。
上单调递增。则正确命题的序号是 。
①④
略

练习册系列答案
相关题目
题目内容
 函数
函数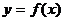
 的导函数
的导函数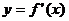 的图象,给出下列命题:
的图象,给出下列命题: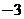 是函数
是函数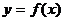 的极值点;
的极值点;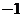 是函数
是函数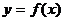 的最小值点;
的最小值点;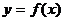 在
在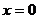 处切线的斜率小于零;
处切线的斜率小于零;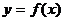 在区间
在区间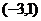 上单调递增。
上单调递增。