题目内容
某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为 ,顶角为
,顶角为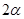 的等腰三角形.
的等腰三角形.
(1)若角 时,求该八边形的面积;
时,求该八边形的面积;
(2)写出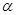 的取值范围,当
的取值范围,当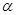 取何值时该八边形的面积最大,并求出最大面积.
取何值时该八边形的面积最大,并求出最大面积.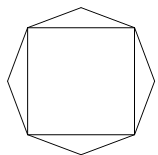
(1) ;(2)
;(2)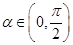 ,当
,当 时,八边形的面积取最大值
时,八边形的面积取最大值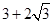 .
.
解析试题分析:(1)先利用 结合余弦定理确定正方形的边长,然后将八边形分为一个正方形与四个等腰三角形求面积,最后将面积相加得到八边形的面积;(2)利用
结合余弦定理确定正方形的边长,然后将八边形分为一个正方形与四个等腰三角形求面积,最后将面积相加得到八边形的面积;(2)利用 得到角
得到角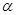 的取值范围,利用正弦定理求出正方形的边长(利用含
的取值范围,利用正弦定理求出正方形的边长(利用含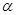 的代数式表示),然后利用面积公式求出八边形的面积关于
的代数式表示),然后利用面积公式求出八边形的面积关于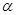 的三角函数,结合降幂公式、辅助角公式将三角函数解析式进行化简,最后求出相应函数在区间
的三角函数,结合降幂公式、辅助角公式将三角函数解析式进行化简,最后求出相应函数在区间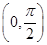 的最大值.
的最大值.
(1)由题可得正方形边长为 ,
, ;
;
(2)显然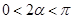 ,所以
,所以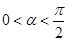 ,
,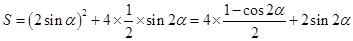
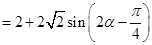 ,
, ,
,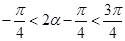 ,故
,故 ,
, 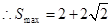 ,此时
,此时 .
.
考点:1.三角形的面积;2.二倍角;3.辅助角公式;4.三角函数的最值

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 ).
).
 ,1),F(
,1),F( ,
, ),求函数f(x)的解析式;
),求函数f(x)的解析式; )满足
)满足 ·
· =
= ,求函数f(x)的最大值.
,求函数f(x)的最大值. 和角
和角 的终边分别与单位圆交于
的终边分别与单位圆交于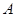 ,
, 两点,(其中
两点,(其中
 ,点
,点 ,求
,求 的值;
的值; , 求
, 求 的值.
的值.
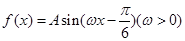 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是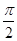 ,且满足,
,且满足,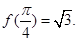
 的单调递减区间;
的单调递减区间; ,求△ABC的面积。
,求△ABC的面积。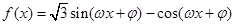 (
(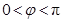 ,
,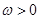 )为偶函数,且函数
)为偶函数,且函数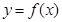 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为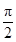 .
.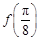 的值;
的值;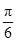 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数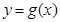 的图象,求
的图象,求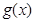 的单调递减区间.
的单调递减区间.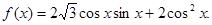
 的值;
的值; 时,求函数
时,求函数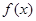 的值域.
的值域.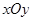 中,点
中,点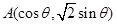 ,
, ,其中
,其中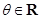 .
. 时,求向量
时,求向量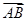 的坐标;
的坐标;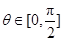 时,求
时,求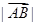 的最大值.
的最大值.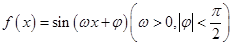 的部分图象如图所示.
的部分图象如图所示.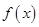 的解析式,并写出
的解析式,并写出 的内角分别是A,B,C,若
的内角分别是A,B,C,若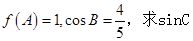 的值.
的值.
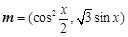 ,
,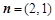 ,函数
,函数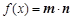 .
.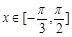 时,求函数
时,求函数 的取值范围;
的取值范围;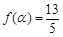 ,且
,且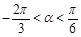 时,求
时,求 的值.
的值.