题目内容
设平面向量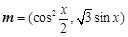 ,
,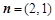 ,函数
,函数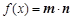 .
.
(1)当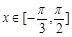 时,求函数
时,求函数 的取值范围;
的取值范围;
(2)当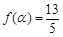 ,且
,且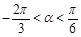 时,求
时,求 的值.
的值.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由向量的坐标运算可得: ,然后降次化一得
,然后降次化一得

 .由
.由 可得
可得 .将
.将 看作一个整体,利用正弦函数的性质便可得
看作一个整体,利用正弦函数的性质便可得 的取值范围.(2)由
的取值范围.(2)由 ,得
,得 ,
, ,所以要求
,所以要求 ,可以用二倍角公式.
,可以用二倍角公式.
(1) 1分
1分
 . 3分
. 3分
当 时,
时, ,则
,则 ,
, ,
,
所以 的取值范围是
的取值范围是 . 6分
. 6分
(2)由 ,得
,得 , 7分
, 7分
因为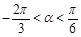 ,所以
,所以 ,得
,得 , 9分
, 9分

 12分
12分
考点:1、三角恒等变换及三角函数求值;2、向量.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 ,顶角为
,顶角为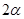 的等腰三角形.
的等腰三角形. 时,求该八边形的面积;
时,求该八边形的面积;  的取值范围,当
的取值范围,当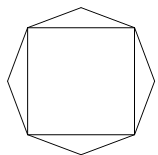
 的终边与单位圆交于点P(
的终边与单位圆交于点P(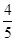 ,
,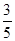 ).
). 、
、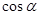 、
、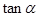 值;
值;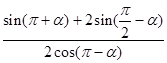 的值.
的值. 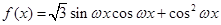 ,
,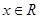 ,
,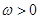 .
.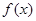 的值域;
的值域; 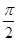 ,则当
,则当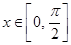 时,求
时,求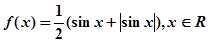
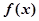 的周期T,与单调增区间.
的周期T,与单调增区间.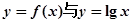 的图象有几个公共交点.
的图象有几个公共交点.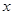 的函数
的函数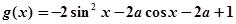 的最小值为
的最小值为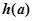 ,试确定满足
,试确定满足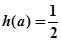 的
的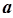 的值,并对此时的
的值,并对此时的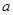 值求
值求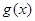 的最小值.
的最小值.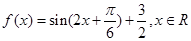 .
. 的最小正周期和单调增区间.
的最小正周期和单调增区间.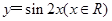 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?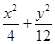 =1上在第一象限的点,A(2,0),B(0,2
=1上在第一象限的点,A(2,0),B(0,2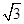 )
)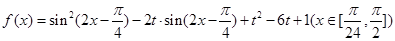 其最小值为
其最小值为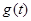 .
.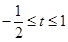 时,要使关于
时,要使关于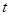 的方程
的方程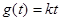 有一个实根,求实数
有一个实根,求实数 的取值范围.
的取值范围.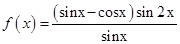 .
.  的定义域及最小正周期;
的定义域及最小正周期;