题目内容
在平面直角坐标系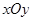 中,点
中,点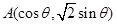 ,
, ,其中
,其中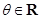 .
.
(1)当 时,求向量
时,求向量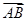 的坐标;
的坐标;
(2)当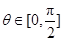 时,求
时,求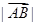 的最大值.
的最大值.
(1)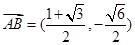 ;(2)
;(2)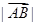 取到最大值
取到最大值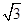 .
.
解析试题分析:(1)求向量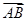 的坐标,由向量坐标的定义可知,
的坐标,由向量坐标的定义可知, ,即可写出
,即可写出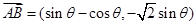 ,再把
,再把 代入求出值即可;(2)求
代入求出值即可;(2)求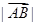 的最大值,先求向量
的最大值,先求向量 的最大值,由于是三角函数,可利用三角函数进行恒等变化,把它变化为一个角的一个三角函数,利用三角函数的性质,即可求出
的最大值,由于是三角函数,可利用三角函数进行恒等变化,把它变化为一个角的一个三角函数,利用三角函数的性质,即可求出 的最大值,从而可得
的最大值,从而可得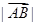 的最大值.
的最大值.
(1)由题意,得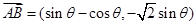 , 2分
, 2分
当  时,
时, , 4分
, 4分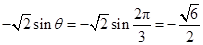 ,
,
所以 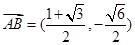 . 6分
. 6分
(2)因为 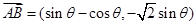 ,
,
所以 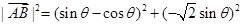 7分
7分 8分
8分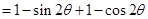 9分
9分 . 10分
. 10分
因为 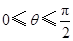 ,
,
所以 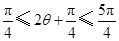 . 11分
. 11分
所以当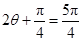 时,
时,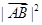 取到最大值
取到最大值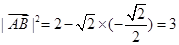 , 12分
, 12分
即当 时,
时,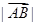 取到最大值
取到最大值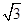 . 13分
. 13分
考点:向量的坐标,向量的模,三角恒等变化.

练习册系列答案
相关题目
已知函数 (A>0,ω>0)的一系列对应值如下表:
(A>0,ω>0)的一系列对应值如下表:
| x | 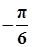 |  | 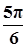 | 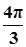 |  |  | 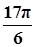 |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数
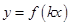 (k>0)周期为
(k>0)周期为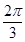 ,当x∈[0,
,当x∈[0, ]时,方程
]时,方程 恰有两个不同的解,求实数m的取值范围;
恰有两个不同的解,求实数m的取值范围; 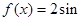
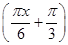
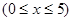 ,点A、B分别是函数
,点A、B分别是函数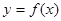 图像上的最高点和最低点.
图像上的最高点和最低点.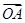 ·
·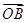 的值;
的值;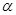 、
、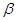 的终边上,求tan(
的终边上,求tan(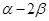 )的值.
)的值. ,顶角为
,顶角为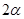 的等腰三角形.
的等腰三角形. 时,求该八边形的面积;
时,求该八边形的面积; 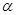 的取值范围,当
的取值范围,当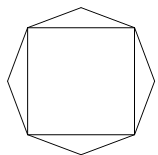
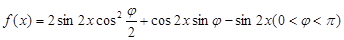 图象的一条对称轴为
图象的一条对称轴为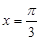 .
.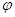 的值;
的值; 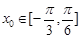 使得
使得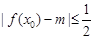 成立,求实数m的取值范围;
成立,求实数m的取值范围;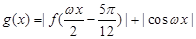 在区间
在区间 上恰有50次取到最大值,求正数
上恰有50次取到最大值,求正数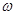 的取值范围.
的取值范围.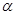 的终边落在直线
的终边落在直线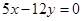 上,求
上,求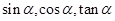 的值。
的值。 的终边与单位圆交于点P(
的终边与单位圆交于点P(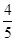 ,
,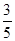 ).
). 、
、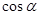 、
、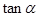 值;
值;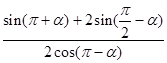 的值.
的值. 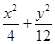 =1上在第一象限的点,A(2,0),B(0,2
=1上在第一象限的点,A(2,0),B(0,2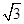 )
) +α),求下列各式的值:
+α),求下列各式的值: ;
;