题目内容
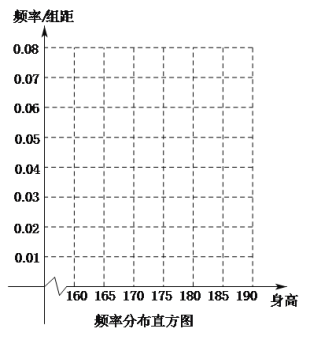
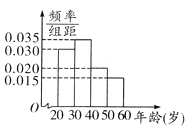
【题目】某工厂有120名工人,其年龄都在20~ 60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分成四组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试。已知各年龄段两项培训结业考试成绩优秀的人数如下表所示。假设两项培训是相互独立的,结业考试也互不影响。
年龄分组 | A项培训成绩 优秀人数 | B项培训成绩 优秀人数 |
[20,30) | 27 | 16 |
[30,40) | 28 | 18 |
[40,50) | 16 | 9 |
[50,60] | 6 | 4 |
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求四个年龄段应分别抽取的人数;
(2)根据频率分布直方图,估计全厂工人的平均年龄;
(3)随机从年龄段[20,30)和[40,50)中各抽取1人,设这两人中A、B两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望.
【答案】(1)12,14,8,6;(2)37岁;(3)见解析.
【解析】分析:(1)由频率分布直方图得各年龄段的频率,分别乘以40即可得人数;
(2)将各年龄段的中点值乘以频率累加可得平均年龄;
(3)先分别计算年龄在[20,30)和年龄段[40,50)的工人A、B两项培训结业考试成绩都优秀的概率,由题设知,X的可能取值为0,1,2,进而求概率可得分布列,利用期望公式可得期望.
详解:(1)由频率分布直方图可知,年龄段[20,30),[30,40),[40,50),[50,60]的人数的频率分别为0.3,0.35,0.2,0.15.
因为40×0.3=12,40×0.35 =14,40×0.2=8,40×0.15 =6,
所以年龄段[20,30),[30,40),[40,50),[50,60]应抽取人数分别为12,14,8,6.
(2)因为各年龄段的中点值分别为25,35,45,55,对应的频率分别为0.3,0.35,0.2,0.15,则25×0.3+35×0.35 +45×0.2+55×0.15= 37.由此估计全厂工人的平均年龄约为37岁.
(3)因为年龄在[20,30)的工人数为120×0.3=36,从该年龄段任取1人,由表知,此人A项培训结业考试成绩优秀的概率为![]() ,B项培训结业考试成绩优秀的概率为
,B项培训结业考试成绩优秀的概率为![]() ,
,
所以A、B两项培训结业考试成绩都优秀的概率为![]() .
.
因为年龄段[40,50)的工人数为120×0.2=24,从该年龄段任取1人,由表知,此人A项培训结业考试成绩优秀的概率为![]() ,B项培训结业考试成绩优秀的概率为
,B项培训结业考试成绩优秀的概率为![]() ,所以A、B两项培训结业考试成绩都优秀的概率为
,所以A、B两项培训结业考试成绩都优秀的概率为![]() .
.
由题设知,X的可能取值为0,1,2.
其中![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列如下表:
X | 0 | 1 | 2 |
P |
|
|
|
所以![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】为了解中学生课余观看热门综艺节目“爸爸去哪儿”是否与性别有关,某中学一研究性学习小组从该校学生中随机抽取了![]() 人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的
人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的![]() ,男生喜欢看该节目的占男生总人数的
,男生喜欢看该节目的占男生总人数的![]() .随后,该小组采用分层抽样的方法从这
.随后,该小组采用分层抽样的方法从这![]() 份问卷中继续抽取了
份问卷中继续抽取了![]() 份进行重点分析,知道其中喜欢看该节目的有
份进行重点分析,知道其中喜欢看该节目的有![]() 人.
人.
(1) 现从重点分析的![]() 人中随机抽取了
人中随机抽取了![]() 人进行现场调查,求这两人都喜欢看该节目的概率;
人进行现场调查,求这两人都喜欢看该节目的概率;
(2) 若有![]() 的把握认为“爱看该节目与性别有关”,则参与调查的总人数
的把握认为“爱看该节目与性别有关”,则参与调查的总人数![]() 至少为多少?
至少为多少?
参考数据:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
【题目】某工厂人员及工资构成如下表:
人员 | 经理 | 管理人员 | 高级技工 | 工人 | 学徒 | 合计 |
周工资/元 | 2200 | 1250 | 1220 | 1200 | 490 | |
人数 | 1 | 6 | 5 | 10 | 1 | 23 |
(1)指出这个问题中的众数、中位数、平均数.
(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么?