题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)当![]() ,
,![]() 时,求证方程
时,求证方程![]() 在区间
在区间![]() 上有唯一实数根;
上有唯一实数根;
(3)当![]() 时,设
时,设![]() 是
是![]() 函数两个不同的极值点,证明:
函数两个不同的极值点,证明:![]() .
.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)构造新函数y=![]() ,求导判断单调性,得出最小值e.(2)变量分离a=-
,求导判断单调性,得出最小值e.(2)变量分离a=-![]() =h(x),根据函数的单调性求出函数h(x)的最小值,利用a的范围证明在区间(0,2)上有唯一实数根;(3)求出
=h(x),根据函数的单调性求出函数h(x)的最小值,利用a的范围证明在区间(0,2)上有唯一实数根;(3)求出![]() ,问题转化为证
,问题转化为证![]() ,令x1﹣x2=t,得到t<0,根据函数的单调性证明即可.
,令x1﹣x2=t,得到t<0,根据函数的单调性证明即可.
(1)当![]() =0,
=0,![]() 时,
时,![]() =
=![]() ,求导y’=
,求导y’=![]() =0的根x=1
=0的根x=1
所以y在(-![]() ),(0,1)递减,在(1,+
),(0,1)递减,在(1,+![]() )递增,
)递增,
所以y![]() =e
=e
(2)![]() +
+![]() =0,所以a=-
=0,所以a=-![]() =h(x)
=h(x)
H’(x)=-![]() =0的根x=2
=0的根x=2
则h(x)在(0,2)上单调递增,在(2,+∞)上单调递减,
所以h(2)是y=h(x)的极大值即最大值,即![]()
所以函数f(x)在区间(0,2)上有唯一实数根;
(3)![]() =
= ![]() -
-![]()
F’(x)![]() -2ax-a=0的两根是
-2ax-a=0的两根是![]() ,
,![]()
∵x1,x2是函数F(x)的两个不同极值点(不妨设x1<x2),
∴a>0(若a≤0时,f'(x)>0,即F(x)是R上的增函数,与已知矛盾),
且F'(x1)=0,F'(x2)=0.∴![]() ,
,![]() …
…
两式相减得: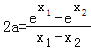 ,…
,…
于是要证明![]() ,即证明
,即证明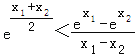 ,两边同除以
,两边同除以![]() ,
,
即证 ,即证
,即证![]() ,即证
,即证![]() ,
,
令x1﹣x2=t,t<0.即证不等式![]() ,当t<0时恒成立.
,当t<0时恒成立.
设![]() ,∴
,∴![]() =
=![]()
设![]() ,∴
,∴![]() ,
,
当t<0,h'(t)<0,h(t)单调递减,
所以h(t)>h(0)=0,即![]() ,
,
∴φ'(t)<0,∴φ(t)在t<0时是减函数.
∴φ(t)在t=0处取得极小值φ(0)=0.
∴φ(t)>0,得证.
∴![]() .
.

【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所有抽取的30岁以上的网民中利用分层抽样抽取5人,
![]() 求这5人中经常使用、偶尔或不用共享单车的人数;
求这5人中经常使用、偶尔或不用共享单车的人数;
![]() 从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 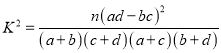 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
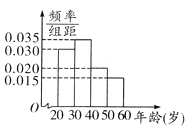
【题目】某工厂有120名工人,其年龄都在20~ 60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分成四组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试。已知各年龄段两项培训结业考试成绩优秀的人数如下表所示。假设两项培训是相互独立的,结业考试也互不影响。
年龄分组 | A项培训成绩 优秀人数 | B项培训成绩 优秀人数 |
[20,30) | 27 | 16 |
[30,40) | 28 | 18 |
[40,50) | 16 | 9 |
[50,60] | 6 | 4 |
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求四个年龄段应分别抽取的人数;
(2)根据频率分布直方图,估计全厂工人的平均年龄;
(3)随机从年龄段[20,30)和[40,50)中各抽取1人,设这两人中A、B两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望.