Question

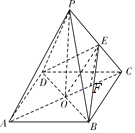
【题目】如图所示，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，底面边长为a，E是PC的中点．

（Ⅰ）求证：PA∥平面BDE；

（Ⅱ）平面PAC⊥平面BDE；

（Ⅲ）若二面角E-BD-C为30°，求四棱锥P-ABCD的体积．

Answer 1

【答案】（I）详见解析；（II）详见解析；（III）.

【解析】

（Ⅰ）连接，证明．然后证明平面

（Ⅱ）证明，，推出平面，然后证明平面⊥平面

（Ⅲ）取中点，连接，说明为二面角的平面角，求出，，．然后求解几何体的体积

解：（Ⅰ）证明：连接OE，如图所示．

∵O、E分别为AC、PC中点，

∴OE∥PA．

∵OE面BDE，PA平面BDE，

∴PA∥平面BDE．

（Ⅱ）证明：∵PO⊥平面ABCD，∴PO⊥BD．

在正方形ABCD中，BD⊥AC，

又∵PO∩AC=O，∴BD⊥平面PAC．

又∵BD平面BDE，∴平面PAC⊥平面BDE．

（Ⅲ）取OC中点F，连接EF．

∵E为PC中点，

∴EF为△POC的中位线，∴EF∥PO．

又∵PO⊥平面ABCD，

∴EF⊥平面ABCD，

∵OF⊥BD，∴OE⊥BD．

∴∠EOF为二面角E-BD-C的平面角，

∴∠EOF=30°．

在Rt△OEF中，

OF=OC=AC=a，

∴EF=OFtan30°=a，∴OP=2EF=a．

∴VP-ABCD=×a2×a=a3．