题目内容
【题目】已知
．
(1)当
＝－1时，求
的单调区间及值域；
(2)若在(
)上为增函数，求实数
的取值范围．
【答案】（1）f(x)的值域为(－∞，2－log23]．增区间为
，减区间为
.（2）
【解析】
(1) 当a＝－1时，f(x)＝log
(x2＋x＋1)，log(x2＋x＋1)≤log
＝2－log23，
∴f(x)的值域为(－∞，2－log23]．由对数式的真数大于0求得函数的定义域，得到内函数的单调区间，结合复合函数的单调性得答案．
(2)用复合函数的单调性来求解，令u(x)＝x2－ax－a＝
2－
－a，
由“若f(x)在
上为增函数，”，可知u(x)应在上为减函数且
u(x)＞0在恒成立．再用“对称轴在区间的右侧，且最小值大于零”求解可得结果．
解 (1)当a＝－1时，f(x)＝log(x2＋x＋1)，
∵x2＋x＋1＝
2＋≥，
∴log(x2＋x＋1)≤log＝2－log23，
∴f(x)的值域为(－∞，2－log23]．
∵y＝x2＋x＋1在
上递减，在
上递增，y＝logx在(0，＋∞)上递减，
∴f(x)的增区间为，
减区间为.
(2)令u(x)＝x2－ax－a＝2－－a，
∵f(x)在
上为单调增函数，
又∵y＝logu(x)为单调减函数，
∴u(x)在上为单调减函数，且u(x)＞0在上恒成立.
因此
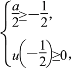即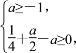
解得－1≤a≤
.
故实数a的取值范围是
.
练习册系列答案
相关题目
