题目内容
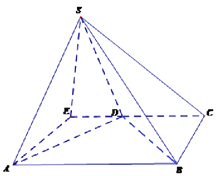
【题目】四棱锥
的底面
为直角梯形，
，
，
，
为正三角形.
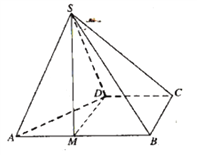
（1）点
为棱
上一点，若
平面
，
，求实数
的值；
（2）求点B到平面SAD的距离.
【答案】（1）
；（2）
【解析】试题分析：（1）由平面，可证
，进而证得四边形
为平行四边形，根据，可得
；
（2）利用等体积法
可求点
到平面
的距离.
试题解析：（（1）因为
平面SDM，
平面ABCD，
平面SDM 
平面ABCD=DM，
所以
，
因为
，所以四边形BCDM为平行四边形，又
，所以M为AB的中点.
因为
，
.
（2）因为
， 
，
所以平面
，
又因为
平面，
所以平面
平面，
平面
平面
，
在平面内过点
作
直线于点
，则平面，
在
和
中，
因为
，所以
，
又由题知
，
所以
，
由已知求得
，所以
，
连接BD，则
，
又求得
的面积为
，
所以由点B 到平面的距离为
.
【题型】解答题
【结束】
19
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作，该公司给出了两种日薪薪酬方案.甲方案：底薪100元，每派送一单奖励1元；乙方案：底薪140元，每日前55单没有奖励，超过55单的部分每单奖励12元.
（1）请分别求出甲、乙两种薪酬方案中日薪
（单位：元）与送货单数
的函数关系式；
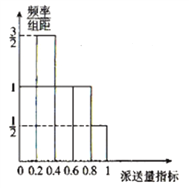
（2）根据该公司所有派送员100天的派送记录，发现派送员的日平均派送单数满足以下条件：在这100天中的派送量指标满足如图所示的直方图，其中当某天的派送量指标在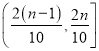
时，日平均派送量为
单.
若将频率视为概率，回答下列问题：
①根据以上数据，设每名派送员的日薪为
（单位：元），试分别求出甲、乙两种方案的日薪
的分布列，数学期望及方差；
②结合①中的数据，根据统计学的思想，帮助小明分析，他选择哪种薪酬方案比较合适，并说明你的理由.
（参考数据： 
， 
， 
， 
， 
， 
， 
， 
， 
）
【答案】（1）
；（2）见解析
【解析】试题分析： 
根据已知条件写出函数关系式，分别求出分布列，然后算出数学期望与方差
运用不同的比较方法求出最优解
解析：（1）甲方案中派送员日薪
（单位：元）与送单数
的函数关系式为： 
，
乙方案中派送员日薪
（单位：元）与送单数
的函数关系式为： 
，
①由已知，在这100天中，该公司派送员日平均派送单数满足如下表格：
单数 | 52 | 54 | 56 | 58 | 60 |
频率 | 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以
的分布列为：
| 152 | 154 | 156 | 158 | 160 |
| 0.2 | 0.3 | 0.2 | 0.2 | 0.1 |
所以
，
，
所以
的分布列为：
| 140 | 152 | 176 | 200 |
| 0.5 | 0.2 | 0.2 | 0.1 |
所以
，
，
②答案一：
由以上的计算可知，虽然
，但两者相差不大，且
远小于
，即甲方案日工资收入波动相对较小，所以小明应选择甲方案.
答案二：
由以上的计算结果可以看出， 
，即甲方案日工资期望小于乙方案日工资期望，所以小明应选择乙方案.
