Question

【题目】已知椭圆，离心率，点在椭圆上．

（1）求椭圆C的标准方程；

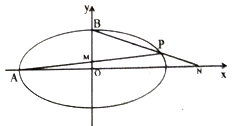
（2）设点P是椭圆C上一点，左顶点为A，上顶点为B，直线PA与y轴交于点M，直线PB与x轴交于点N，求证： 为定值．

Answer 1

【答案】（1）；（2）见解析.

【解析】试题分析：（1）根据椭圆的离心率，点在椭圆上，结合性质 ，列出关于 、 、的方程组，求出 、 、，即可得椭圆C的标准方程；（2）设 ，根据三点共线斜率相等，可分别求出 的坐标，利用两点间的距离公式可将用 表示，结合点在椭圆上消去 即可得结果.

试题解析：（1）依题意得，设，则，

由点在椭圆上，有，解得，则，

椭圆C的方程为：

设，，，则，由APM三点共线，则有，即，解得，则，

由BPN三点共线，有，即，解得，

则

=

又点P在椭圆上，满足，有，

代入上式得

=，

可知为定值。