题目内容
【题目】如图4,四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,交
,交![]() 于点
于点![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)由![]() 平面
平面![]() ,得到
,得到![]() ,再由四边形
,再由四边形![]() 为正方形得到
为正方形得到![]() ,从而证明
,从而证明![]() 平面
平面![]() ,从而得到
,从而得到![]() ,再结合
,再结合![]() ,即
,即![]() 以及直线与平面垂直的判定定理证明
以及直线与平面垂直的判定定理证明![]() 平面
平面![]() ;(2)先证明
;(2)先证明![]() 、
、![]() 、
、![]() 三条直线两两垂直,然后以点
三条直线两两垂直,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,利用空间向量法求出二面角
轴建立空间直角坐标系,利用空间向量法求出二面角![]() 的余弦值.
的余弦值.
试题解析:(1)![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ;
;
(2)设![]() ,则
,则![]() 中,
中,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,由(1)知
,由(1)知![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,同理
,同理![]() ,
,
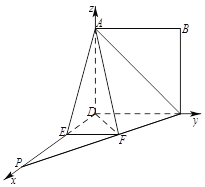
如图所示,以![]() 为原点,建立空间直角坐标系,则
为原点,建立空间直角坐标系,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则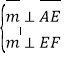 ,又
,又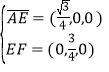 ,
,
所以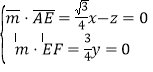 ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
由(1)知平面![]() 的一个法向量
的一个法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,可知
,可知![]() 为锐角,
为锐角,
![]()
![]() ,即所求.
,即所求.

【题目】我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
分组 | 频数 | 频率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | |
[80,90) | ||
[90,100] | 14 | 0.28 |
合计 | 1.00 |
如果用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,再从6人中选2人,求2人分数都在[80,90)的概率.

【题目】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.



