题目内容
【题目】已知函数
(I)求函数f(x)的最小正周期和对称中心的坐标
(II)设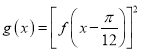
,求函数g(x)在
上的最大值,并确定此时x的值
【答案】(I) 
， 
. (II) 见解析.
【解析】试题分析：(Ⅰ)由二倍角公式和化一公式化简可得
；
(Ⅱ)由(Ⅰ)知
的解析式,把
代入求
,进而求出g(x),结合x的范围,求出最大值即可.
试题解析：(I) 
∴函数f(x)的最小正周期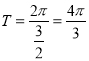
，
由
，得
，
∴函数f(x)的对称中心的坐标为
.
(II)由(I)可得f(x－
)＝2sin[
(x－)＋
]＝2sin(x＋
)，
∴g(x)＝[f(x－)]2＝4×
＝2－2cos(3x＋)，
∵x∈[－
，
]，∴－≤3x＋≤
，
∴当3x＋＝π，即x＝时，g(x)max＝4.
点睛:三角函数式的化简要遵循“三看”原则:（1）一看“角”，这是最重要的一环，通过看角之间的区别和联系，把角进行合理的拆分，从而正确使用公式；（2）而看“函数名称”看函数名称之间的差异，从而确定使用公式，常见的有“切化弦”；（3）三看“结构特征”，分析结构特征，可以帮助我们找到变形的方向，如“遇到分式通分”等.
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
【题目】甲、乙两名运动员的5次测试成绩如下图所示：
甲 | 茎 | 乙 |
5 7 | 1 | 6 8 |
8 8 2 | 2 | 3 6 7 |
设s1 ， s2分别表示甲、乙两名运动员测试成绩的标准差， 
分别表示甲、乙两名运动员测试成绩的平均数，则有（ ）
A.
，s1＜s2
B. ，s1＞s2
C.
，s1＞s2
D. ，s1=s2
