题目内容
(本小题满分12分)
如图所示,点 在圆
在圆 :
: 上,
上,
 轴,点
轴,点 在射线
在射线 上,且满足
上,且满足
 .
.

(Ⅰ)当点 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹 的方程,并根据
的方程,并根据 取值说明轨迹
取值说明轨迹 的形状.
的形状.
(Ⅱ)设轨迹 与
与 轴正半轴交于点
轴正半轴交于点 ,与
,与 轴正半轴交于点
轴正半轴交于点 ,直线
,直线 与轨迹
与轨迹 交于点
交于点 、
、 ,点
,点 在直线
在直线 上,满足
上,满足 ,求实数
,求实数 的值.
的值.
如图所示,点
 在圆
在圆 :
: 上,
上,
 轴,点
轴,点 在射线
在射线 上,且满足
上,且满足
 .
.
(Ⅰ)当点
 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹 的方程,并根据
的方程,并根据 取值说明轨迹
取值说明轨迹 的形状.
的形状.(Ⅱ)设轨迹
 与
与 轴正半轴交于点
轴正半轴交于点 ,与
,与 轴正半轴交于点
轴正半轴交于点 ,直线
,直线 与轨迹
与轨迹 交于点
交于点 、
、 ,点
,点 在直线
在直线 上,满足
上,满足 ,求实数
,求实数 的值.
的值.(1)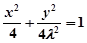 ;
;
当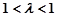 时,轨迹
时,轨迹 表示焦点在
表示焦点在 轴上的椭圆;当
轴上的椭圆;当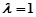 时轨迹
时轨迹 就是圆O;
就是圆O;
当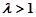 时轨迹
时轨迹 表示焦点是
表示焦点是 轴上的椭圆.
轴上的椭圆.
(2)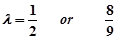
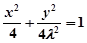 ;
;当
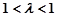 时,轨迹
时,轨迹 表示焦点在
表示焦点在 轴上的椭圆;当
轴上的椭圆;当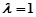 时轨迹
时轨迹 就是圆O;
就是圆O;当
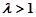 时轨迹
时轨迹 表示焦点是
表示焦点是 轴上的椭圆.
轴上的椭圆.(2)
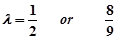
本试题主要是考查了轨迹方程的求解,以及直线与呀unzhuiquxiand位置关系的综合运用。利用对称性和向量的关系来建立坐标关系并求解。
(1)因为设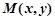 、
、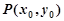 ,由于
,由于 和
和
 轴,所以
轴,所以
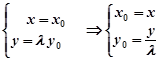 代入圆方程得:
代入圆方程得: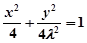
(2)由题设知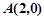 ,
,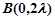 ,
, ,
, 关于原点对称,所以设
关于原点对称,所以设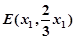 ,
,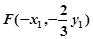 ,
,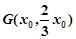 ,不妨设
,不妨设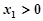 分别计算得到G,E的坐标,结合向量关系得到结论。
分别计算得到G,E的坐标,结合向量关系得到结论。
解:(1)设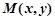 、
、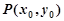 ,由于
,由于 和
和
 轴,所以
轴,所以
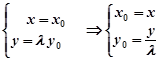 代入圆方程得:
代入圆方程得: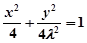 --------------2分
--------------2分
当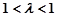 时,轨迹
时,轨迹 表示焦点在
表示焦点在 轴上的椭圆;当
轴上的椭圆;当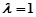 时轨迹
时轨迹 就是圆O;
就是圆O;
当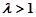 时轨迹
时轨迹 表示焦点是
表示焦点是 轴上的椭圆.
轴上的椭圆. ---------------4分
---------------4分
(2)由题设知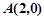 ,
,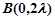 ,
, ,
, 关于原点对称,所以设
关于原点对称,所以设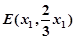 ,
,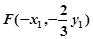 ,
,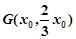 ,不妨设
,不妨设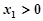 ---------------6分
---------------6分
直线 的方程为:
的方程为: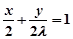 把点
把点 坐标代入得
坐标代入得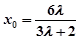
又, 点 在轨迹
在轨迹 上,则有
上,则有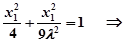
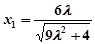 -------8分
-------8分
∵ 即
即 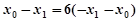
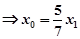 -----------10分
-----------10分
∴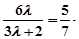
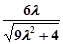 (
(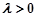 )
)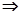
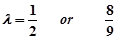 ----------12分
----------12分
(1)因为设
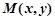 、
、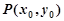 ,由于
,由于 和
和
 轴,所以
轴,所以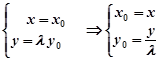 代入圆方程得:
代入圆方程得: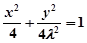
(2)由题设知
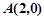 ,
,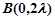 ,
, ,
, 关于原点对称,所以设
关于原点对称,所以设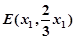 ,
,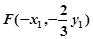 ,
,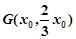 ,不妨设
,不妨设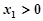 分别计算得到G,E的坐标,结合向量关系得到结论。
分别计算得到G,E的坐标,结合向量关系得到结论。解:(1)设
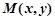 、
、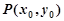 ,由于
,由于 和
和
 轴,所以
轴,所以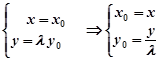 代入圆方程得:
代入圆方程得: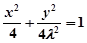 --------------2分
--------------2分当
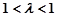 时,轨迹
时,轨迹 表示焦点在
表示焦点在 轴上的椭圆;当
轴上的椭圆;当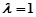 时轨迹
时轨迹 就是圆O;
就是圆O;当
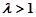 时轨迹
时轨迹 表示焦点是
表示焦点是 轴上的椭圆.
轴上的椭圆. ---------------4分
---------------4分(2)由题设知
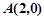 ,
,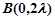 ,
, ,
, 关于原点对称,所以设
关于原点对称,所以设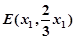 ,
,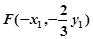 ,
,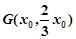 ,不妨设
,不妨设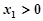 ---------------6分
---------------6分直线
 的方程为:
的方程为: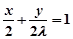 把点
把点 坐标代入得
坐标代入得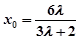
又, 点
 在轨迹
在轨迹 上,则有
上,则有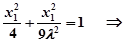
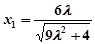 -------8分
-------8分∵
 即
即 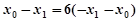
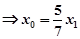 -----------10分
-----------10分∴
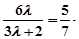
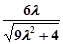 (
(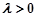 )
)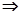
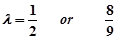 ----------12分
----------12分
练习册系列答案
相关题目

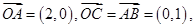 动点
动点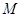 到定直线
到定直线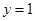 的距离等于
的距离等于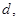 并且满足
并且满足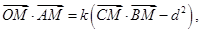 其中
其中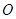 是坐标原点,
是坐标原点,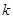 是参数.
是参数.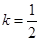 时,求
时,求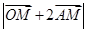 的最大值和最小值;
的最大值和最小值;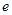 满足
满足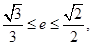 求实数
求实数 的左焦点为
的左焦点为 ,
, 是两个顶点,如果
是两个顶点,如果 的距离等于
的距离等于 ,则椭圆的离心率为 .
,则椭圆的离心率为 . 是曲线
是曲线 上任意一点,则点
上任意一点,则点 的最小距离是( )
的最小距离是( ) 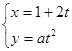 ,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。
,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。 >b>
>b> 的离心率为
的离心率为 且椭圆的一个焦点与抛物线
且椭圆的一个焦点与抛物线 的焦点重合,斜率为
的焦点重合,斜率为 的直线
的直线 过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).
过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴相交于点M(0,m).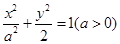 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,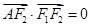 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为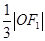 .
.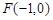 ,交 y 轴于点M,若
,交 y 轴于点M,若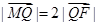 ,求直线l 的斜率.
,求直线l 的斜率.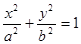 (
(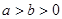 )的右焦点为
)的右焦点为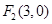 ,离心率为
,离心率为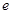 .
.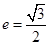 ,求椭圆的方程;
,求椭圆的方程;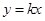 与椭圆相交于
与椭圆相交于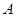 ,
,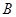 两点,
两点,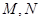 分别为线段
分别为线段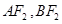 的中点. 若坐标原点
的中点. 若坐标原点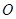 在以
在以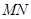 为直径的圆上,且
为直径的圆上,且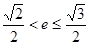 ,求
,求 的取值范围.
的取值范围.