题目内容
【题目】已知函数f (x)=ex+2x2-3x.
(1)求证:函数f (x)在区间[0,1]上存在唯一的极值点.
(2)当x≥![]() 时,若关于x的不等式f (x)≥
时,若关于x的不等式f (x)≥![]() x2+(a-3)x+1恒成立,试求实数a的取值范围.
x2+(a-3)x+1恒成立,试求实数a的取值范围.
【答案】(1)见解析.
(2) ![]() .
.
【解析】分析:(1)先求f′(0)与f′(1),看两值是否异号,然后证明f′(x)在[0,1]上单调性,即可证明函数f(x)在区间[0,1]上存在唯一的极值点;
(2)由题意得到ex-![]() ,x2-ax-1≥0,构造g(x)=ex-
,x2-ax-1≥0,构造g(x)=ex-![]() x2-ax-1,分类讨论求出g(x)的最值,即可得到a的范围.
x2-ax-1,分类讨论求出g(x)的最值,即可得到a的范围.
详解:(1)f ′(x)=ex+4x-3,
∵f ′(0)=e0-3=-2<0,f ′(1)=e+1>0,
∴f ′(0)·f ′(1)<0.
令h(x)=f ′(x)=ex+4x-3,则h′(x)=ex+4>0,
∴f ′(x)在区间[0,1]上单调递增,
∴f ′(x)在区间[0,1]上存在唯一零点,
∴f(x)在区间[0,1]上存在唯一的极小值点.
(2)由f(x)≥![]() x2+(a-3)x+1,得ex+2x2-3x≥
x2+(a-3)x+1,得ex+2x2-3x≥![]() x2+(a-3)x+1,即ax≤ex-
x2+(a-3)x+1,即ax≤ex-![]() x2-1,
x2-1,
∵x≥![]() ,∴a≤
,∴a≤![]()
令g(x)=![]() ,则g′(x)=
,则g′(x)=![]()
令φ(x)=ex(x-1)-![]() x2+1,则φ′(x)=x(ex-1).∵x≥
x2+1,则φ′(x)=x(ex-1).∵x≥![]() ,∴φ′(x)>0.
,∴φ′(x)>0.
∴φ(x)在[![]() ,+∞)上单调递增.∴φ(x)≥φ(
,+∞)上单调递增.∴φ(x)≥φ(![]() )=
)=![]() -
-![]()
![]() >0.
>0.
因此g′(x)>0,故g(x)在[![]() ,+∞)上单调递增,
,+∞)上单调递增,
则g(x)≥g(![]() )=
)=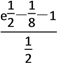 =2
=2![]() -
-![]() ,∴a的取值范围是a≤2
,∴a的取值范围是a≤2![]() -
-![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目