题目内容
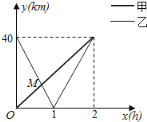
【题目】在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,根据图象解答以下问题:
之间的函数图象,根据图象解答以下问题:
![]() 直接写出
直接写出![]() ,
,![]() 与x之间的函数关系式
与x之间的函数关系式![]() 不必写过程
不必写过程![]() ,求出点M的坐标,并解释该点坐标所表示的实际意义;
,求出点M的坐标,并解释该点坐标所表示的实际意义;
![]() 若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
![]() 若甲乙两人离A地的距离之积为
若甲乙两人离A地的距离之积为![]() ,求出函数
,求出函数![]() 的表达式,并求出它的最大值.
的表达式,并求出它的最大值.
【答案】(1)M(![]() ,
,![]() ),甲乙经过
),甲乙经过![]() h第一次相遇,此时离A距离
h第一次相遇,此时离A距离![]() km;(2)甲乙两人能够用无线对讲机保持联系;(3)可得f(x)的最大值为f(2)=1600.
km;(2)甲乙两人能够用无线对讲机保持联系;(3)可得f(x)的最大值为f(2)=1600.
【解析】
试题(1)由图形,结合一次函数的解析式的求法,可得所求解析式;再令y甲=y乙,求得M的坐标,进而得到几何意义;
(2)令y甲﹣y乙≤5,解不等式可得x的范围,进而得到所求结论;
(3)运用分段函数的形式写出f(x),再由二次函数的最值的求法,即可得到所求的最大值.
解:(1)y甲=20x,0≤x≤2;y乙=![]() ,
,
令y甲=y乙,可得20x=40﹣40x,解得x=![]() ,
,
进而y甲=y乙=![]() ,即有M(
,即有M(![]() ,
,![]() ),
),
M的坐标表示:甲乙经过![]() h第一次相遇,此时离A距离
h第一次相遇,此时离A距离![]() km;
km;
(2)乙返回过程中,当1<x≤2时,乙与甲相距5km之内,
即y甲﹣y乙≤5,即为20x﹣(40x﹣40)≤5,解得x≥![]() ,即
,即![]() ≤x≤2,
≤x≤2,
则(2﹣![]() )×60=15分钟,甲乙两人能够用无线对讲机保持联系;
)×60=15分钟,甲乙两人能够用无线对讲机保持联系;
(3)f(x)=![]() =
=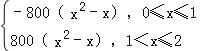
=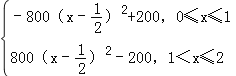 ,
,
当0<x≤1时,f(x)的最大值为f(![]() )=200;
)=200;
当1<x≤2时,f(x)递增,f(2)为最大值,且为1600.
综上可得f(x)的最大值为f(2)=1600.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目