题目内容
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,
,![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
【答案】(1)6x+2y-1=0;(2)g(x)在x=0处取得极小值g(0)=-3,在x=3处取得极大值g(3)=15e-3.
【解析】试题分析:(Ⅰ)由已知条件解出a,b,得到函数f(x)的表达式,切线方程的斜率即为该点导数值,由点斜式即可写出切线方程;
(Ⅱ)求g(x)导函数g′(x)=(-3x2+9x)e-x,可得出单调区间,从而得到极值.
试题解析:(1)∵f(x)=x3+ax2+bx+1,∴f′(x)=3x2+2ax+b,
则![]() 解得
解得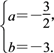
∴f(x)=x3-![]() x2-3x+1,∴f(1)=-
x2-3x+1,∴f(1)=-![]() ,f′(1)=-3,
,f′(1)=-3,
∴y=f(x)在(1,f(1))处的切线方程为
y-![]() =-3(x-1),即6x+2y-1=0;
=-3(x-1),即6x+2y-1=0;
(2)由(1)知g(x)=(3x2-3x-3)e-x,
∴g′(x)=(-3x2+9x)e-x,
令g′(x)=0,即(-3x2+9x)e-x=0,得x=0或x=3,
当x∈(-∞,0)时,g′(x)<0,
故g(x)在(-∞,0)上单调递减.
当x∈(0,3)时,g′(x)>0,故g(x)在(0,3)上单调递增.
当x∈(3,+∞)时,g′(x)<0,
故g(x)在(3,+∞)上单调递减.
从而函数g(x)在x=0处取得极小值g(0)=-3,
在x=3处取得极大值g(3)=15e-3.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】[2019·龙泉驿区一中]交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,且保费与上一年车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个以及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了70辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 13 | 7 | 20 | 14 | 6 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损6000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有7辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次性购进70辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值(结果用分数表示).