Question

【题目】已知函数 ，g（x）=2ln（x+m）．
（1）当m=0，存在x0∈[ ，e]（e为自然对数的底数），使 ，求实数a的取值范围；
（2）当a=m=1时，设H（x）=xf（x）+g（x），在H（x）的图象上是否存在不同的两点A（x1 ， y1），B（x2 ， y2）（x1＞x2＞﹣1），使得H（x1）﹣H（x2）= ？请说明理由．

Answer 1

【答案】
（1）解：x0f（x0）≥g（x0）可化为 ，

令h（x）=x2﹣2lnx，则

∴当x∈ 时，h'（x）＜0；当x∈（1，e]时，h'（x）＞0；

又∵ ，∴ ，则a≤e2﹣2

（2）解：H（x）=x2+2ln（x+1）﹣1， ；

；

；

故可化为 = ，即 =

又即 = ①，

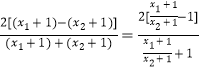令 ，①式可化为 ，

令 ， ，∴u（t）在（1，+∞）上递增

∴u（t）≥u（1）=0；∴u（t）无零点，故A、B两点不存在

【解析】（1）x0f（x0）≥g（x0）可化为 ， 构造h（x）=x2﹣2lnx，求出其值域即可．（2） ； ；
故可化为 = ，即 =
又即 = ①，
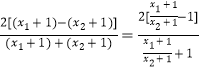令 ，①式可化为
令 ， ，只需考查u（t）的值域即可．
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本，需要知道一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．