题目内容
设函数f(x)=x-2msin x+(2m-1)sin xcos x(m为实数)在(0,π)上为增函数,则m的取值范围为( )
A.[0, ] ] | B.(0, ) ) | C.(0, ] ] | D.[0, ) ) |
A
∵f(x)在区间(0,π)上是增函数,
∴f′(x)=1-2mcos x+2(m-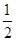 )cos 2x
)cos 2x
=2[(2m-1)cos2x-mcos x+1-m]
=2(cos x-1)[(2m-1)cos x+(m-1)]>0
在(0,π)上恒成立,令cos x=t,则-1<t<1,
即不等式(t-1)[(2m-1)t+(m-1)]>0在(-1,1)上恒成立,
①若m>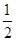 ,则t<
,则t<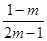 在(-1,1)上恒成立,
在(-1,1)上恒成立,
则只需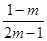 ≥1,即
≥1,即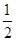 <m≤
<m≤ ,
,
②当m=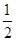 时,则0·t+
时,则0·t+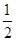 -1<0,
-1<0,
在(-1,1)上显然成立;
③若m<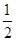 ,则t>
,则t>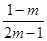 在(-1,1)上恒成立,
在(-1,1)上恒成立,
则只需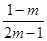 ≤-1,即0≤m<
≤-1,即0≤m<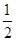 .
.
综上所述,所求实数m的取值范围是[0, ].
].
∴f′(x)=1-2mcos x+2(m-
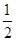 )cos 2x
)cos 2x=2[(2m-1)cos2x-mcos x+1-m]
=2(cos x-1)[(2m-1)cos x+(m-1)]>0
在(0,π)上恒成立,令cos x=t,则-1<t<1,
即不等式(t-1)[(2m-1)t+(m-1)]>0在(-1,1)上恒成立,
①若m>
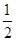 ,则t<
,则t<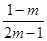 在(-1,1)上恒成立,
在(-1,1)上恒成立,则只需
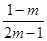 ≥1,即
≥1,即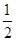 <m≤
<m≤ ,
,②当m=
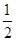 时,则0·t+
时,则0·t+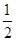 -1<0,
-1<0,在(-1,1)上显然成立;
③若m<
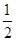 ,则t>
,则t>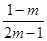 在(-1,1)上恒成立,
在(-1,1)上恒成立,则只需
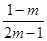 ≤-1,即0≤m<
≤-1,即0≤m<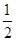 .
.综上所述,所求实数m的取值范围是[0,
 ].
].
练习册系列答案
相关题目
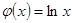
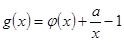 在点
在点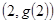 处的切线与直线
处的切线与直线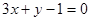 平行,求
平行,求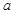 的值;
的值;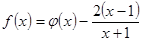 在
在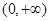 上为单调增函数;
上为单调增函数;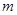 ,
, ,且
,且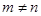 ,求证:
,求证: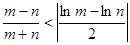 .
. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数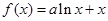 ,对任意的
,对任意的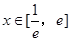 时,
时,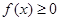 恒成立,则a的范围为 .
恒成立,则a的范围为 .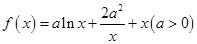 .若曲线
.若曲线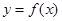 在点
在点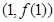 处的切线与直线
处的切线与直线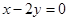 垂直,
垂直,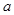 的值;
的值;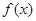 的单调区间;
的单调区间;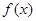 满足
满足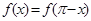 且当
且当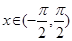 时,
时,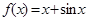 ,则( )
,则( )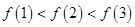
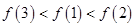
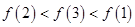
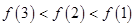
 .
. 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求实数
成立,求实数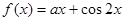 在区间
在区间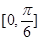 上是单调函数,则实数
上是单调函数,则实数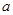 的取值范围是( )
的取值范围是( )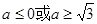
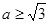
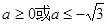
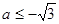
 x2
x2 ㏑x的单调递减区间为( )
㏑x的单调递减区间为( ) 1,1]
1,1]