题目内容
13.已知函数f(x)=ln(x+1)-ax(a∈R).(1)若曲线y=f(x)过点P(1,ln2-1),求曲线y=f(x)在点P处的切线方程;
(2)讨论f(x)在定义域上的单调性;
(3)是否存在常数a∈N,使得a≥(1+$\frac{1}{x}$)x对任意正实数x都成立?若存在,试求出a的最小值并证明你的结论;若不存在,请说明理由.
分析 (1)由曲线过P,可得a=1,求出函数的导数,求得切线的斜率,由点斜式方程可得切线方程;
(2)求出导数,对a讨论,a=0,a>0,a<0,令导数大于0,可得增区间,令导数小于0,可得减区间;
(3)由(2)可得a=1有x∈(0,+∞)时,ln(1+x)<x恒成立.$\frac{1}{x}$代换ln(1+x)<x中的x得,ln(1+$\frac{1}{x}$)<$\frac{1}{x}$,再取x=2可得2<(1+$\frac{1}{x}$)x<e,即可得到a的最小值.
解答 解:(1)由曲线y=f(x)过点P(1,ln2-1),
知f(1)=ln2-a=ln2-1,所以a=1,
因为f(x)=ln(x+1)-x,f′(x)=$\frac{1}{x+1}$-1,
所以f′(1)=-$\frac{1}{2}$,
所以切线方程为y=-$\frac{1}{2}$x+ln2-$\frac{1}{2}$;
(2)因为f′(x)=$\frac{1}{x+1}$-a=$\frac{1-ax-a}{x+1}$,
令f′(x)>0,得1-ax-a>0,即ax<1-a,
①当a=0时,f(x)在(-1,+∞)单调递增,
②当a>0时,f(x)在(-1,$\frac{1-a}{a}$)单调递增,在($\frac{1-a}{a}$,+∞)单调递减,
③当a<0时,因为$\frac{1-a}{a}$<-1,所以f(x)在(-1,+∞)单调递增,
综上,当a≤0时,f(x)在(-1,+∞)单调递增;
当a>0时,f(x)在(-1,$\frac{1-a}{a}$)单调递增,在($\frac{1-a}{a}$,+∞)单调递减.
(3)由(2)知当a=1时,f(x)在(-1,0)内单调递增,在(0,+∞)内单调递减,
所以当x∈(0,+∞)时,f(x)<f(0)=0,
即当x∈(0,+∞)时,ln(1+x)<x恒成立.
$\frac{1}{x}$代换ln(1+x)<x中的x得,ln(1+$\frac{1}{x}$)<$\frac{1}{x}$,
所以xln(1+$\frac{1}{x}$)<1,
即ln(1+$\frac{1}{x}$)x<1,所以(1+$\frac{1}{x}$)x<e,
取x=2时,(1+$\frac{1}{x}$)x=$\frac{9}{4}$>2,
所以amin=3.
点评 本题考查导数的运用:求切线方程和单调区间,同时考查不等式恒成立问题,注意运用单调性和分类讨论的思想方法是解题的关键.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案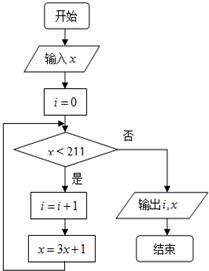 运行如图所示的程序流程图.
运行如图所示的程序流程图.(1)若输入x的值为2,根据该程序的运行过程填写下面的表格,并求输出i与x的值;
| 第i次 | i=1 | i=2 | i=3 | i=4 | i=5 |
| x= | 7 | 22 | 67 | 202 | 607 |
(3)若输出i的值为2,求输入x的取值范围.
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
| A. | 120 | B. | -30 | C. | 15 | D. | -15 |
| x(平方米) | 80 | 90 | 100 | 110 |
| y(万元) | 42 | 46 | 53 | 59 |
(2)若在该市购买120平方米的房屋,估计购房费用是多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.