题目内容

正方体ABCD-A1B1C1D1的棱长为1，点M在AB上，且AM=
1
3
，点P是平面ABCD上的动点，且动点P到直线A1D1的距离与动点P到点M的距离的平方差为1，则动点的轨迹是（　　）
A．圆B．抛物线C．双曲线D．直线
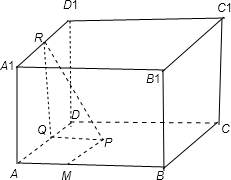
如图所示：正方体ABCD-A1B1C1D1 中，作PQ⊥AD，Q为垂足，则PQ⊥面ADD1A1，过点Q作QR⊥D1A1，
则D1A1⊥面PQR，PR即为点P到直线A1D1的距离，由题意可得 PR2-PQ2=RQ2=1．
又已知 PR2-PM2=1，∴PM=PQ，即P到点M的距离等于P到AD的距离，根据抛物线的定义可得，点P的轨迹是抛物线，
故选 B．
练习册系列答案
相关题目
方程
(x+3)2+(y-1)2
=|x-y+3|表示的曲线是（　　）
A．圆B．椭圆C．双曲线D．抛物线
已知动点P（x，y）与两定点M（-1，0），N（1，0）连线的斜率之积等于常数λ（λ≠0）．
（I）求动点P的轨迹C的方程；
（II）试根据λ的取值情况讨论轨迹C的形状．
过原点O的椭圆有一个焦点F（0，4），且长轴长2a=10，求此椭圆的中心的轨迹方程．
在平面直角坐标系xOy中，点P到两点（0，-
3
），（0，
3
）的距离之和等于4，设点P的轨迹为C．
（1）写出C的方程；
（2）设直线y=kx+1与C交于A，B两点．k为何值时以AB为直径的圆经过原点O？此时|AB|的值是多少？
若M、N为两个定点且|MN|=6，动点P满足
PM
•
PN
=0，则P点的轨迹是（　　）
A．圆B．椭圆C．双曲线D．抛物线
已知点O（0，0），A（1，-2），动点P满足|PA|=3|PO|，则点P的轨迹方程是（　　）
A．8x2+8y2+2x-4y-5=0B．8x2+8y2-2x-4y-5=0
C．8x2+8y2-2x+4y-5=0D．8x2+8y2+2x+4y-5=0
如图，已知定点A（1，0），定圆C：（x+1）2+y2=8，M为圆C上的一个动点，点P在线段AM上，点N在线段CM上，且满足
AM
=2
AP
，
NP
•
AM
=0，则点N的轨迹方程是______．
已知定点A(-
3
，0)，B(
3
，0)，动点P（x，y）满足：||AP|-|BP||=2；
（1）求动点P的轨迹方程；
（2）直线mx-y+1=0与动点P的轨迹只有一个交点，求实数m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网