题目内容
已知定点A(-
,0),B(
,0),动点P(x,y)满足:||AP|-|BP||=2;
(1)求动点P的轨迹方程;
(2)直线mx-y+1=0与动点P的轨迹只有一个交点,求实数m的值.
| 3 |
| 3 |
(1)求动点P的轨迹方程;
(2)直线mx-y+1=0与动点P的轨迹只有一个交点,求实数m的值.
(1)∵定点A(-
,0),B(
,0),动点P(x,y)满足:||AP|-|BP||=2,
∴||AP|-|BP||=2<|AB|=2
,
∴动点P的轨迹是A、B为焦点的双曲线,且a=1,c=
,
∴b=
=
,
∴动点P的轨迹方程是x2-
=1;
(2)由mx-y+1=0可得y=mx+1,
代入x2-
=1,可得x2-
=1,
即(2-m2)x2-2mx-3=0.
①2-m2=0,即m=±
时,方程只有一个解,满足题意;
②2-m2≠0时,△=4m2+12(2-m2)=0,解得m=±
,
综上所述,m=m=±
或m=±
.
| 3 |
| 3 |
∴||AP|-|BP||=2<|AB|=2
| 3 |
∴动点P的轨迹是A、B为焦点的双曲线,且a=1,c=
| 3 |
∴b=
| c2-a2 |
| 2 |
∴动点P的轨迹方程是x2-
| y2 |
| 2 |
(2)由mx-y+1=0可得y=mx+1,
代入x2-
| y2 |
| 2 |
| (mx+1)2 |
| 2 |
即(2-m2)x2-2mx-3=0.
①2-m2=0,即m=±
| 2 |
②2-m2≠0时,△=4m2+12(2-m2)=0,解得m=±
| 3 |
综上所述,m=m=±
| 2 |
| 3 |

练习册系列答案
相关题目
 的左,右两个顶点分别为
的左,右两个顶点分别为 、
、 .曲线
.曲线 是以
是以 的双曲线.设点
的双曲线.设点 在第一象限且在曲线
在第一象限且在曲线 与椭圆相交于另一点
与椭圆相交于另一点 .
. ,
, ,证明:
,证明: .
. +y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )
+y2=1的左、右焦点,P是第一象限内该椭圆上的一点,且PF1⊥PF2,则点P的横坐标为( )


 +
+ =1的焦点在x轴上,过点(1,
=1的焦点在x轴上,过点(1,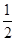 )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________.
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________.