题目内容
【题目】已知数列{an}，{bn}满足a1=1，a2=2，b1=2，且对任意的正整数i，j，k，l，当i+j=k+l时，都有ai+bj=ak+bl ， 则 
的值是（ ）
A.2012
B.2013
C.2014
D.2015
【答案】D
【解析】解：∵i+j=k+l时，都有ai+bj=ak+bl ，
则 
= 
= 
×2013
=a1+b2013
∵a1=1，a2=2，b1=2，
∴a1+b2=a2+b1
∴b2=3
同理可得，b3=a2+b2﹣a1=4
b4=a2+b3﹣a1=5
…
∴b2013=2014
=a1+b2013=2015
即 =2015
故选D
【考点精析】认真审题，首先需要了解等差数列的前n项和公式(前n项和公式：
)，还要掌握等比数列的前n项和公式(前
项和公式：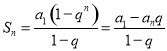
)的相关知识才是答题的关键．
练习册系列答案
相关题目
