Question

【题目】在三棱锥P﹣ABC中，PA=PB=PC= ，侧棱PA与底面ABC所成的角为60°，则该三棱锥外接球的体积为 ．

Answer 1

【答案】
【解析】解：过点P作PH⊥平面ABC于H，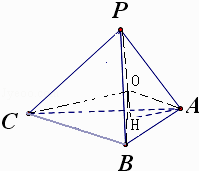
则∵AH是PA在平面ABC内的射影，
∴∠PAH是直线PA与底面ABC所成的角，得∠PAH=60°，
∴Rt△PAH中，AH=PAcos60°= ，PH=PAsin60°= ，
设三棱锥外接球的球心为O，∵PA=PB=PC，
∴P在平面ABC内的射影H是△ABC的外心，
由此可得，外接球心O必定在PH上，连接OA、OB、OC
∵△POA中，OP=OA，
∴∠OAP=∠OPA=30°，可得PA= OA=
∴三棱锥外接球的半径R=OA=1．
因此该三棱锥外接球的体积为V= πR3= ，
所以答案是： ．