题目内容
【题目】设数列{an}的前n项和为Sn ， a1=1，且nan+1=（n+2）Sn ， n∈N* ．
（1）求证：数列 
为等比数列；
（2）求数列{Sn}的前n项和Tn ．
【答案】
（1）证明：∵nan+1=（n+2）Sn，n∈N*．∴n（Sn+1﹣Sn）=（n+2）Sn，∴ 
=2× 
，
∴数列 
为等比数列，首项为1，公比为2，
（2）解：由（1）可得： =2n﹣1，∴Sn=n2n﹣1．
∴数列{Sn}的前n项和Tn=1+2×2+3×2n+…+n2n﹣1．
∴2Tn=2+2×22+…+（n﹣1）2n﹣1+n2n，
∴﹣Tn=1+2+22+…+2n﹣1﹣n2n= 
﹣n2n，
∴Tn=（n﹣1）2n+1．
【解析】（1）nan+1=（n+2）Sn ， n∈N* ． 可得n（Sn+1﹣Sn）=（n+2）Sn ， 变形为 =2× ，即可证明．（2）由（1）可得： =2n﹣1 ， 可得Sn=n2n﹣1 ． 利用“错位相减法”、等比数列的求和公式即可得出．
【考点精析】认真审题，首先需要了解等比数列的通项公式（及其变式）(通项公式：
)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系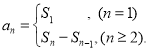
)的相关知识才是答题的关键．
练习册系列答案
相关题目
