Question

【题目】如图，正方体ABCD-A1B1C1D1 ， O是底面ABCD对角线的交点．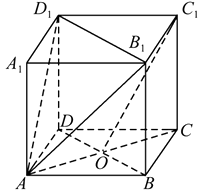

求证：（I） C1O∥面AB1D1；
（II）面A1C⊥面AB1D1 ．

Answer 1

【答案】解：(I)连结 ，设 连结 ，

是正方体，四边形 是平行四边形 ∴A1C1∥AC且

又 分别是 ，AC的中点，∴ 且 ,,,

四边形 是平行四边形 ． , 面 面 ,∴ ∥面

（II）在正方体中，AA1⊥平面A1B1C1D1，

平面A1B1C1D1，

在平面A1B1C1D1内， ,

，

， ,

,

面A1C⊥面AB1D1 ．

【解析】(1)根据已知作出辅助线由四边形是平行四边形可得C 1 O / / AO1 ,再结合线面平行的判定定理即可得证。(2)由已知的线线垂直得证D1B1⊥面A1C，再利用面面垂直的判定定理即可得证。