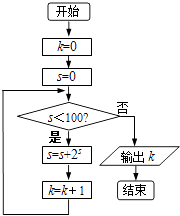
题目内容
【题目】如图,直三棱柱ABC﹣A1B1C1中,CA=CB,M,N,P分别为AB,A1C1 , BC的中点. 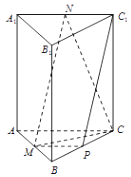
求证:
(1)C1P∥平面MNC;
(2)平面MNC⊥平面ABB1A1 .
【答案】
(1)证明:连接MP,因为M、P分别为AB,BC的中点
∵MP∥AC,MP= ![]() ,
,
又因为在直三棱柱ABC﹣A1B1C1中,∴AC∥A1C1,AC=A1C1
且N是A1C1的中点,∴MP∥C1N,MP=C1N
∴四边形MPC1N是平行四边形,∴C1P∥MN
∵C1P面MNC,MN面MNC,∴C1P∥平面MNC;
(2)证明:在△ABC中,CA=CB,M为AB的中点,∴CM⊥AB.
在直三棱柱ABC﹣A1B1C1中,B1B⊥面ABC.
∵CM面ABC,∴BB1⊥CM
由因为BB1∩AB=B,BB1,AB平面面ABB1A1
又CM平面MNC,
∴平面MNC⊥平面ABB1A1.
【解析】(1)连接MP,只需证明四边形MPC1N是平行四边形,即可得MN∥C1P∵C1P,即可证得C1P∥平面MNC;(2)只需证明CM⊥平面MNC,即可得平面MNC⊥平面ABB1A1.

【题目】某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | a | 0.9 |
第3组 | [35,45) | 27 | x |
第4组 | [45,55) | b | 0.36 |
第5组 | [55,65) | 3 | y |
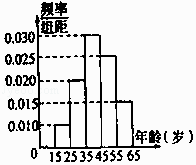
(1)分别求出a,b,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.