题目内容
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() )图象上两个相邻的最值点为
)图象上两个相邻的最值点为![]() 和
和![]()
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 在区间
在区间![]() 上的对称中心、对称轴;
上的对称中心、对称轴;
(3)将函数![]() 图象上每一个点向右平移
图象上每一个点向右平移![]() 个单位得到函数
个单位得到函数![]() ,令
,令![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值,并指出此时x的值.
上的最大值,并指出此时x的值.
【答案】(1)![]() ;(2)
;(2) ![]() 在区间
在区间![]() 上的对称中心为
上的对称中心为![]() ,对称轴为
,对称轴为![]() ; (3)
; (3)![]() 在区间
在区间![]() 上的最大值为2,此时
上的最大值为2,此时![]() .
.
【解析】
(1)由函数的顶点坐标求出![]() ,由周期求出
,由周期求出![]() ,由五点作图法求出
,由五点作图法求出![]() ,可得函数
,可得函数![]() 的解析式;
的解析式;
(2)利用正弦函数的图像的对称性,可得函数![]() 在区间
在区间![]() 上的对称中心、对称轴;
上的对称中心、对称轴;
(3)根据函数![]() 的图像变换规律,利用三角恒等变换可得
的图像变换规律,利用三角恒等变换可得![]() 的解析式,利用正弦函数的定义域与值域,可得函数
的解析式,利用正弦函数的定义域与值域,可得函数![]() 在区间
在区间![]() 上的最大值与此时x的值.
上的最大值与此时x的值.
解:(1)由函数![]() (
(![]() ,
,![]() ,
,![]() )图象上两个相邻的最值点为
)图象上两个相邻的最值点为![]() 和
和![]() ,可得
,可得![]() ,
, ![]() ,可得
,可得![]() ,
,
再根据五点作图法,可得![]() ,
,![]() ,故
,故![]() ;
;
(2)令![]() ,可得
,可得![]() ,故可得函数的对称中心为
,故可得函数的对称中心为![]() ,可得
,可得![]() 在区间
在区间![]() 上的对称中心为
上的对称中心为![]() ;
;
令![]() ,可得
,可得![]() ,故可得函数的对称轴为
,故可得函数的对称轴为![]() ,可得
,可得![]() 在区间
在区间![]() 上的对称轴为为
上的对称轴为为![]() ;
;
(3)由函数![]() 图象上每一个点向右平移
图象上每一个点向右平移![]() 个单位得到函数
个单位得到函数![]() ,可得
,可得![]() ,故可得:
,故可得:![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() 取得最大值2,此时
取得最大值2,此时![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市环保部门对该市市民进行了一次动物保护知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参'与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 15 | 5 | 10 |
若规定问卷得分不低于70分的市民称为“动物保护关注者”,则山图中表格可得![]() 列联表如下:
列联表如下:
非“动物保护关注者” | 是“动物保护关注者” | 合计 | |
男 | 10 | 45 | 55 |
女 | 15 | 30 | 45 |
合计 | 25 | 75 | 100 |
(1)请判断能否在犯错误的概率不超过0.05的前提下认为“动物保护关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“动物保护达人”.现在从本次调查的“动物保护达人”中利用分层抽样的方法随机抽取6名市民参与环保知识问答,再从这6名市民中抽取2人参与座谈会,求抽取的2名市民中,既有男“动物保护达人”又有女“动物保护达人”的概率.
附表及公式: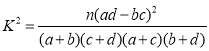 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |