题目内容
【题目】已知函数f(x)=ln![]() .
.
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)对于x∈[2,6],f(x)=ln![]() >ln
>ln![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1) (-∞,-1)∪(1,+∞),奇函数.(2) 0<m<7.
【解析】
(1)解不等式![]() >0,即得函数的定义域.再利用奇偶函数的判定方法判断函数的奇偶性.(2)转化成以0<m<(x+1)(7-x)在x∈[2,6]上恒成立.再求出函数的最小值得解.
>0,即得函数的定义域.再利用奇偶函数的判定方法判断函数的奇偶性.(2)转化成以0<m<(x+1)(7-x)在x∈[2,6]上恒成立.再求出函数的最小值得解.
(1)由![]() >0,解得x<-1或x>1,
>0,解得x<-1或x>1,
所以函数f(x)的定义域为(-∞,-1)∪(1,+∞),
当x∈(-∞,-1)∪(1,+∞)时,
f(-x)=ln![]() =ln
=ln![]() =ln
=ln![]() =-ln
=-ln![]() =-f(x),
=-f(x),
所以f(x)=ln![]() 是奇函数.
是奇函数.
(2)由于x∈[2,6]时,
f(x)=ln![]() >ln
>ln![]() 恒成立,
恒成立,
所以![]() >
>![]() >0,
>0,
因为x∈[2,6],所以0<m<(x+1)(7-x)在x∈[2,6]上恒成立.
令g(x)=(x+1)(7-x)=-(x-3)2+16,x∈[2,6],
由二次函数的性质可知,x∈[2,3]时函数g(x)单调递增,x∈[3,6]时函数g(x)单调递减,
即x∈[2,6]时,g(x)min=g(6)=7,
所以0<m<7.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案【题目】某市环保部门对该市市民进行了一次动物保护知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参'与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 15 | 5 | 10 |
若规定问卷得分不低于70分的市民称为“动物保护关注者”,则山图中表格可得![]() 列联表如下:
列联表如下:
非“动物保护关注者” | 是“动物保护关注者” | 合计 | |
男 | 10 | 45 | 55 |
女 | 15 | 30 | 45 |
合计 | 25 | 75 | 100 |
(1)请判断能否在犯错误的概率不超过0.05的前提下认为“动物保护关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“动物保护达人”.现在从本次调查的“动物保护达人”中利用分层抽样的方法随机抽取6名市民参与环保知识问答,再从这6名市民中抽取2人参与座谈会,求抽取的2名市民中,既有男“动物保护达人”又有女“动物保护达人”的概率.
附表及公式: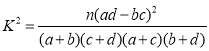 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |