Question

【题目】在平面直角坐标系中,点是曲线上的动点, 到点的距离与到直线的距离相等.

（Ⅰ）求曲线的方程;

（Ⅱ）设是曲线上的点,点在曲线上,直线分别与轴交于点,且,求直线的斜率.

Answer 1

【答案】（Ⅰ）；（Ⅱ） .

【解析】试题分析：（Ⅰ）由抛物线的定义知曲线是以为焦点的抛物线，故可得曲线方程；（Ⅱ）设的直线方程为, ，联立直线与抛物线的方程，求出直线的方程求出，同理可求出，因为,所以，结合韦达定理化简即可得，故而可得最后结论.

试题解析：（Ⅰ）由抛物线的定义知,曲线是以为焦点,以为准线的抛物线所以,所以,所以曲线的方程为.

（Ⅱ）设的直线方程为,

由消去,得，则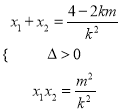

因为点,,所以直线的方程为:

令,则，同理:

因为,所以,即,而

所以

即

所以

化简得:

所以，综上:直线的斜率为.