题目内容
【题目】对于无穷数列![]() ,记
,记![]() ,若数列
,若数列![]() 满足:“存在
满足:“存在![]() ,使得只要
,使得只要![]() (
(![]() 且
且![]() ),必有
),必有![]() ”,则称数列
”,则称数列![]() 具有性质
具有性质![]() .
.
(Ⅰ)若数列![]() 满足
满足![]() 判断数列
判断数列![]() 是否具有性质
是否具有性质![]() ?是否具有性质
?是否具有性质![]() ?
?
(Ⅱ)求证:“![]() 是有限集”是“数列
是有限集”是“数列![]() 具有性质
具有性质![]() ”的必要不充分条件;
”的必要不充分条件;
(Ⅲ)已知![]() 是各项为正整数的数列,且
是各项为正整数的数列,且![]() 既具有性质
既具有性质![]() ,又具有性质
,又具有性质![]() ,求证:存在整数
,求证:存在整数![]() ,使得
,使得![]() 是等差数列.
是等差数列.
【答案】(Ⅰ)数列![]() 不具有性质
不具有性质![]() ;具有性质
;具有性质![]() ;(Ⅱ)见解析;(Ⅲ)见解析.
;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析:(1)根据新定义直接验证即可的结论(2)对于“![]() 是有限集”是“数列
是有限集”是“数列![]() 具有性质
具有性质![]() ”的必要不充分条件,先证不充分性对于周期数列
”的必要不充分条件,先证不充分性对于周期数列![]() ,
, ![]() 是有限集,但是由于
是有限集,但是由于![]() ,
,
所以不具有性质![]() ;再证必要性因为数列
;再证必要性因为数列![]() 具有性质
具有性质![]() ,所以一定存在一组最小的
,所以一定存在一组最小的![]() 且
且![]() ,满足
,满足![]() ,即
,即![]() ,所以数列
,所以数列![]() 中必然会以某个周期进行,所以数列
中必然会以某个周期进行,所以数列![]() 中最多有
中最多有![]() 个不同的项,从而得证(3)因为数列
个不同的项,从而得证(3)因为数列![]() 具有性质
具有性质![]() ,数列
,数列![]() 具有性质
具有性质![]() ,所以存在
,所以存在![]() ,使得
,使得![]() ,
, ![]() ,其中
,其中![]() 分别是满足上述关系式的最小的正整数,然后根据其性质列出相关等式可得结论,然后逐一分析取值讨论
分别是满足上述关系式的最小的正整数,然后根据其性质列出相关等式可得结论,然后逐一分析取值讨论
试题解析:
(Ⅰ)数列![]() 不具有性质
不具有性质![]() ;具有性质
;具有性质![]() .
.
(Ⅱ)(不充分性)对于周期数列![]() ,
, ![]() 是有限集,但是由于
是有限集,但是由于![]() ,
,
所以不具有性质![]() ;
;
(必要性)因为数列![]() 具有性质
具有性质![]() ,
,
所以一定存在一组最小的![]() 且
且![]() ,满足
,满足![]() ,即
,即![]()
由性质![]() 的含义可得
的含义可得![]()
所以数列![]() 中,从第k项开始的各项呈现周期性规律:
中,从第k项开始的各项呈现周期性规律: ![]() 为一个周期中的各项,
为一个周期中的各项,
所以数列![]() 中最多有
中最多有![]() 个不同的项,
个不同的项,
所以![]() 最多有
最多有![]() 个元素,即
个元素,即![]() 是有限集.
是有限集.
(Ⅲ)因为数列![]() 具有性质
具有性质![]() ,数列
,数列![]() 具有性质
具有性质![]() ,
,
所以存在![]() ,使得
,使得![]() ,
, ![]() ,其中
,其中![]() 分别是满足上述关系式的最小的正整数,
分别是满足上述关系式的最小的正整数,
由性质![]() 的含义可得
的含义可得![]() ,
, ![]() ,
,
若![]() ,则取
,则取![]() ,可得
,可得![]() ;
;
若![]() ,则取
,则取![]() ,可得
,可得![]() .
.
记![]() ,则对于
,则对于![]() ,有
,有![]() ,
, ![]() ,显然
,显然![]() ,
,
由性质![]() 的含义可得
的含义可得![]() ,
, ![]() ,
,
所以![]()
![]()
所以![]() .
.
所以![]() ,
,
又![]() 是满足
是满足![]() ,
, ![]() 的最小的正整数,
的最小的正整数,
所以![]() ,
,
![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
取![]() ,则
,则![]() ,
,
所以,若![]() 是偶数,则
是偶数,则![]() ;
;
若![]() 是奇数,则
是奇数,则![]() ,
,
所以![]() ,
, ![]()
所以![]() 是公差为1的等差数列.
是公差为1的等差数列.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】某公司为评估两套促销活动方案(方案1运作费用为5元/件;方案2的运作费用为2元/件),在某地区部分营销网点进行试点(每个试点网点只采用一种促销活动方案),运作一年后,对比该地区上一年度的销售情况,制作相应的等高条形图如图所示.
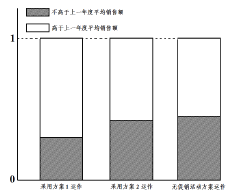
(1)请根据等高条形图提供的信息,为该公司今年选择一套较为有利的促销活动方案(不必说明理由);
(2)已知该公司产品的成本为10元/件(未包括促销活动运作费用),为制定本年度该地区的产品销售价格,统计上一年度的8组售价![]() (单位:元/件,整数)和销量
(单位:元/件,整数)和销量![]() (单位:件)(
(单位:件)(![]() )如下表所示:
)如下表所示:
售价 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
销量 | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①请根据下列数据计算相应的相关指数![]() ,并根据计算结果,选择合适的回归模型进行拟合;
,并根据计算结果,选择合适的回归模型进行拟合;
②根据所选回归模型,分析售价![]() 定为多少时?利润
定为多少时?利润![]() 可以达到最大.
可以达到最大.
|
|
| |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
(附:相关指数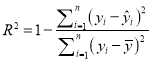 )
)