Question

【题目】等腰直角三角形ABC的直角顶点A在x轴的正半轴上，B在y轴的正半轴上，C在第一象限，设∠BAO=θ（O为坐标原点），AB=AC=2，当OC的长取得最大值时，tanθ的值为（ ）
A.
B.﹣1+
C.
D.

Answer 1

【答案】A
【解析】解：由题意画出图象如图所示：
过点C做x轴的垂线，垂足为D，AB=AC=2，
在RT△ABO中，∠BAO=θ，则OA=2cosθ，
∵∠BAC= ，∴∠ACD=θ，
在RT△ACD中，AD=2sinθ，CD=2cosθ，
∴OD=OA+AD=2（sinθ+cosθ），
则OC2=OD2+CD2=4（1+sin2θ）+4cos2θ
=6+4sin2θ+2cos2θ=6+2 sin（2θ+α），
其中 ， ，
当sin（2θ+α）=1时，OC的长取得最大值，
即 ，则 ，
∴ ， ，
则 ，
∴ ，解得tanθ= ，则tanθ= ，
故选：A．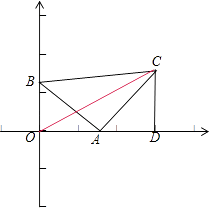

【考点精析】本题主要考查了两角和与差的正切公式的相关知识点，需要掌握两角和与差的正切公式：才能正确解答此题．