题目内容
【题目】如图已知椭圆C: ![]() +y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N.
+y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N. 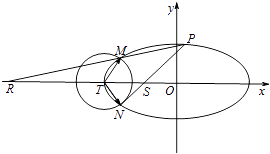
(1)求 ![]() 的最小值;
的最小值;
(2)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:丨OR丨丨OS丨为定值.
【答案】
(1)解:依题意,得a=2,b=1,c= ![]() =
= ![]() ,T(﹣2,0).
,T(﹣2,0).
点M与点N关于x轴对称,
设M(x1,y1),N(x1,﹣y1),不妨设y1>0.
由于点M在椭圆C上,∴ ![]() =1﹣
=1﹣ ![]() ,(*)
,(*)
![]() =(x1+2,y1),
=(x1+2,y1), ![]() =(x1+2,﹣y1),
=(x1+2,﹣y1),
∴ ![]() =(x1+2)2﹣
=(x1+2)2﹣ ![]()
= 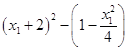 =
= ![]() ﹣
﹣ ![]() ,
,
由于﹣2<x1<2,
故当 ![]() 时,
时, ![]() 取得最小值为﹣
取得最小值为﹣ ![]()
(2)证明:设P(x0,y0),
则直线MP的方程为:y﹣y0= ![]() (x﹣x0),
(x﹣x0),
令y=0,得xR= ![]() ,
,
同理:xS= ![]() ,
,
故xRxS= ![]() ,(**)
,(**)
又点M与点P在椭圆上,故 ![]() ,
, ![]() =4
=4 ![]() ,
,
代入(**)式,得:xRxS= 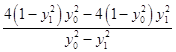 =
= 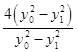 =4.
=4.
∴丨OR丨丨OS丨=|xRxS|=4为定值
【解析】(1)T(﹣2,0).点M与点N关于x轴对称,设M(x11),N(x1 , ﹣y1),不妨设y1>0.由于点M在椭圆C上, ![]() =1﹣
=1﹣ ![]() ,可得
,可得 ![]() =
= ![]() ﹣
﹣ ![]() ,由于﹣2<x1<2,可得
,由于﹣2<x1<2,可得 ![]() 取得最小值.(2)设P(x0 , y0),则直线MP的方程为:y﹣y0=
取得最小值.(2)设P(x0 , y0),则直线MP的方程为:y﹣y0= ![]() (x﹣x0),令y=0,得xR=
(x﹣x0),令y=0,得xR= ![]() ,同理:xS=
,同理:xS= ![]() ,xRxS=
,xRxS= ![]() ,又点M与点P在椭圆上,故
,又点M与点P在椭圆上,故 ![]() ,
, ![]() =4
=4 ![]() ,代入丨OR丨丨OS丨=|xRxS|,化简即可证明.
,代入丨OR丨丨OS丨=|xRxS|,化简即可证明.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

