ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨΈΣΤάΙάΝΫΧΉ¥ΌœζΜνΕ·ΖΫΑΗΘ®ΖΫΑΗ1‘ΥΉςΖ―”ΟΈΣ5‘Σ/ΦΰΘΜΖΫΑΗ2ΒΡ‘ΥΉςΖ―”ΟΈΣ2‘Σ/ΦΰΘ©Θ§‘ΎΡ≥ΒΊ«χ≤ΩΖ÷”ΣœζΆχΒψΫχ–– ‘ΒψΘ®ΟΩΗω ‘ΒψΆχΒψ÷Μ≤…”Ο“Μ÷÷¥ΌœζΜνΕ·ΖΫΑΗΘ©Θ§‘ΥΉς“ΜΡξΚσΘ§Ε‘±»ΗΟΒΊ«χ…œ“ΜΡξΕ»ΒΡœζ έ«ιΩωΘ§÷ΤΉςœύ”ΠΒΡΒ»ΗΏΧθ–ΈΆΦ»γΆΦΥυ ΨΘ°
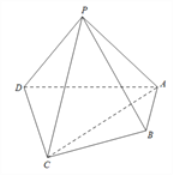
Θ®1Θ©«κΗυΨίΒ»ΗΏΧθ–ΈΆΦΧαΙ©ΒΡ–≈œΔΘ§ΈΣΗΟΙΪΥΨΫώΡξ―Γ‘ώ“ΜΧΉΫœΈΣ”–άϊΒΡ¥ΌœζΜνΕ·ΖΫΑΗΘ®≤Μ±ΊΥΒΟςάμ”…Θ©ΘΜ
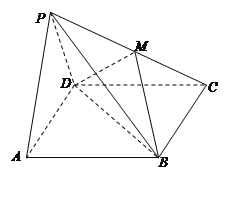
Θ®2Θ©“―÷ΣΗΟΙΪΥΨ≤ζΤΖΒΡ≥…±ΨΈΣ10‘Σ/ΦΰΘ®Έ¥Αϋά®¥ΌœζΜνΕ·‘ΥΉςΖ―”ΟΘ©Θ§ΈΣ÷ΤΕ®±ΨΡξΕ»ΗΟΒΊ«χΒΡ≤ζΤΖœζ έΦέΗώΘ§Ά≥ΦΤ…œ“ΜΡξΕ»ΒΡ8Ήι έΦέ![]() Θ®ΒΞΈΜΘΚ‘Σ/ΦΰΘ§’ϊ ΐΘ©ΚΆœζΝΩ
Θ®ΒΞΈΜΘΚ‘Σ/ΦΰΘ§’ϊ ΐΘ©ΚΆœζΝΩ![]() Θ®ΒΞΈΜΘΚΦΰΘ©Θ®
Θ®ΒΞΈΜΘΚΦΰΘ©Θ®![]() Θ©»γœ¬±μΥυ ΨΘΚ
Θ©»γœ¬±μΥυ ΨΘΚ
έΦέ | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
œζΝΩ | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
ΔΌ«κΗυΨίœ¬Ν– ΐΨίΦΤΥψœύ”ΠΒΡœύΙΊ÷Η ΐ![]() Θ§≤ΔΗυΨίΦΤΥψΫαΙϊΘ§―Γ‘ώΚœ ΒΡΜΊΙιΡΘ–ΆΫχ––ΡβΚœΘΜ
Θ§≤ΔΗυΨίΦΤΥψΫαΙϊΘ§―Γ‘ώΚœ ΒΡΜΊΙιΡΘ–ΆΫχ––ΡβΚœΘΜ
ΔΎΗυΨίΥυ―ΓΜΊΙιΡΘ–ΆΘ§Ζ÷Έω έΦέ![]() Ε®ΈΣΕύ…Ό ±ΘΩάϊ»σ
Ε®ΈΣΕύ…Ό ±ΘΩάϊ»σ![]() Ω…“‘¥οΒΫΉν¥σ.
Ω…“‘¥οΒΫΉν¥σ.
|
|
| |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
Θ®ΗΫΘΚœύΙΊ÷Η ΐ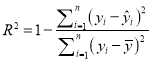 Θ©
Θ©
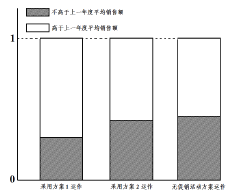
ΓΨ¥πΑΗΓΩΘ®1Θ©ΡξΕ»ΤΫΨυœζ έΕν”κΖΫΑΗ1ΒΡ‘ΥΉςœύΙΊ–‘«Ω”ΎΖΫΑΗ2.Θ®2Θ©ΔΌ≤…”ΟΜΊΙιΡΘ–Ά![]() Ϋχ––ΡβΚœΉνΈΣΚœ . ΔΎ
Ϋχ––ΡβΚœΉνΈΣΚœ . ΔΎ![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”…Β»ΗΏΧθ–ΈΆΦΩ…≈–ΕœΡξΕ»ΤΫΨυœζ έΕν”κΖΫΑΗ1ΒΡ‘ΥΉςœύΙΊ–‘«Ω”ΎΖΫΑΗ2.
Θ®2Θ©ΔΌ”…“―÷Σ ΐΨίΩ…÷ΣΘ§ ![]() ±»Ϋœ¥σ–ΓΩ…ΒΟΉνΦ―ΡβΚœΖΫΑΗ;
±»Ϋœ¥σ–ΓΩ…ΒΟΉνΦ―ΡβΚœΖΫΑΗ;
ΔΎ”…Θ®1Θ©Ω…÷ΣΘ§≤…”ΟΖΫΑΗ1ΒΡ‘ΥΉς–ßΙϊΫœΖΫΑΗ2ΚΟΘ§Ι Ρξάϊ»σ![]() Θ§«σΒΦ«σΉν÷ΒΦ¥Ω….
Θ§«σΒΦ«σΉν÷ΒΦ¥Ω….
‘ΧβΫβΈωΘΚΘ®1Θ©”…Β»ΗΏΧθ–ΈΆΦΩ…÷ΣΘ§ΡξΕ»ΤΫΨυœζ έΕν”κΖΫΑΗ1ΒΡ‘ΥΉςœύΙΊ–‘«Ω”ΎΖΫΑΗ2.
Θ®2Θ©ΔΌ”…“―÷Σ ΐΨίΩ…÷ΣΘ§ΜΊΙιΡΘ–Ά![]() Ε‘”ΠΒΡœύΙΊ÷Η ΐ
Ε‘”ΠΒΡœύΙΊ÷Η ΐ![]() ΘΜ
ΘΜ
ΜΊΙιΡΘ–Ά![]() Ε‘”ΠΒΡœύΙΊ÷Η ΐ
Ε‘”ΠΒΡœύΙΊ÷Η ΐ![]() ΘΜ
ΘΜ
ΜΊΙιΡΘ–Ά![]() Ε‘”ΠΒΡœύΙΊ÷Η ΐ
Ε‘”ΠΒΡœύΙΊ÷Η ΐ![]() .
.
“ρΈΣ![]() Θ§Υυ“‘≤…”ΟΜΊΙιΡΘ–Ά
Θ§Υυ“‘≤…”ΟΜΊΙιΡΘ–Ά![]() Ϋχ––ΡβΚœΉνΈΣΚœ .
Ϋχ––ΡβΚœΉνΈΣΚœ .
ΔΎ”…Θ®1Θ©Ω…÷ΣΘ§≤…”ΟΖΫΑΗ1ΒΡ‘ΥΉς–ßΙϊΫœΖΫΑΗ2ΚΟΘ§
Ι Ρξάϊ»σ![]() Θ§
Θ§ ![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§ ![]() ΒΞΒςΒί‘ωΘΜ
ΒΞΒςΒί‘ωΘΜ
Β±![]() ±Θ§
±Θ§ ![]() ΒΞΒςΒίΦθΘ§
ΒΞΒςΒίΦθΘ§
Ι Β± έΦέ![]() ±Θ§άϊ»σ¥οΒΫΉν¥σ.
±Θ§άϊ»σ¥οΒΫΉν¥σ.

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ