题目内容
8．
如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的面积为πab，随机向矩形区域内投掷一飞镖，则飞镖落入椭圆区域内的概率是$\frac{π}{4}$．
分析 利用几何概型公式，所求为椭圆面积与矩形的面积比．
解答 解：由几何概型公式得飞镖落入椭圆区域内的概率是$\frac{{S}_{椭圆}}{{S}_{矩形}}$=$\frac{πab}{4ab}=\frac{π}{4}$；
故答案为：$\frac{π}{4}$．
点评 本题考查了几何概型公式的运用；关键是明确所求为面积比．
练习册系列答案
相关题目
18．
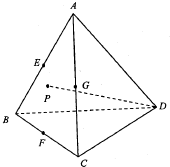如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点，点P在侧面ABC及其边界上运动，DP⊥AB，则动点P的轨迹是（ ）
如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点，点P在侧面ABC及其边界上运动，DP⊥AB，则动点P的轨迹是（ ）| A． | 线段FG | B． | 线段EG | C． | 线段EF | D． | 线段EC |
在一段时间内有100辆汽车经过某交通岗，有2辆汽车速度小于35km/h，有3辆汽车的速度大于75km/h，时速（单位：km/h）频率分布直方图如图所示，
3．要从编号为1，2，3…，60的某种型号冰箱中随机抽取6台进行检测，用系统抽样的方法确定所选取的6台冰箱的编号可能是（ ）
| A． | 5，10，15，20，25，30 | B． | 3，13，23，33，43，53 | ||
| C． | 1，2，3，4，5，6 | D． | 2，4，8，16，32，48 |
13．集合A={x|x≥1}，B={x|x＜m}，若A∪B=R，则m的最小值是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
17．
如图所示的图形由两个等腰直角三角形和一个正方形组成，且正方形的边长为2，直线x=t（0＜t≤4）从左到右扫过图形的面积为S=f（t），则$f（\frac{1}{4}）+f（\frac{3}{2}）$等于（ ）
如图所示的图形由两个等腰直角三角形和一个正方形组成，且正方形的边长为2，直线x=t（0＜t≤4）从左到右扫过图形的面积为S=f（t），则$f（\frac{1}{4}）+f（\frac{3}{2}）$等于（ ）| A． | $\frac{11}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{29}{16}$ | D． | $\frac{33}{16}$ |