题目内容
6.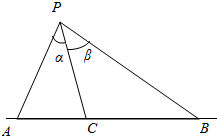 如图,一条直线上有三点A,B,C,点C在点A与点B之间,点P是此直线外一点,设∠APC=α,∠BPC=β.求证:$\frac{sin(α+β)}{PC}=\frac{sinα}{PB}+\frac{sinβ}{PA}$.
如图,一条直线上有三点A,B,C,点C在点A与点B之间,点P是此直线外一点,设∠APC=α,∠BPC=β.求证:$\frac{sin(α+β)}{PC}=\frac{sinα}{PB}+\frac{sinβ}{PA}$.
分析 过点C作CE∥PA,交PB于点E,利用两直线平行内错角相等得到∠PCE=∠APC,∠PEC=π-(α+β),利用正弦定理列出关系式,再结合比例性质,即可证明结论.
解答  证明:过点C作CE∥PA,交PB于点E,则∠PCE=α,∠PEC=π-(α+β),
证明:过点C作CE∥PA,交PB于点E,则∠PCE=α,∠PEC=π-(α+β),
则在△PCE中,由正弦定理得:$\frac{sin∠PEC}{PC}$=$\frac{sin∠PCE}{PE}$=$\frac{sin∠BPC}{CE}$,
即$\frac{sin[π-(α+β)]}{PC}$=$\frac{sinα}{PE}$=$\frac{sinβ}{CE}$,
∴$\frac{sin(α+β)}{PC}$=$\frac{PA•sinα}{PA•PE}$=$\frac{PB•sinβ}{PB•CE}$,
利用比例性质,有:$\frac{sin(α+β)}{PC}$=$\frac{PAsinα+PBsinβ}{PA•PE+PB•CE}$,
∵CE∥PA,
∴CE:PA=BE:PB,
∴PA•PE+PB•CE=PA•PE+PA•BE=PA•(PE+BE)=PA•PB,
则$\frac{sin(α+β)}{PC}$=$\frac{sinα}{PB}$+$\frac{sinβ}{PA}$.
点评 本题考查正弦定理,比例的性质,以及诱导公式的作用,熟练掌握正弦定理是解本题的关键..

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 已知A、B两监测点间距离为3400米,且两点到同一爆炸声的时间差为6s,且B处的声强是A处声强的4倍,声强与距离的平方成反比,求爆炸点P到两监测点中点Q的距离(精确到1m,声速为340m/s).
已知A、B两监测点间距离为3400米,且两点到同一爆炸声的时间差为6s,且B处的声强是A处声强的4倍,声强与距离的平方成反比,求爆炸点P到两监测点中点Q的距离(精确到1m,声速为340m/s).