题目内容
14.是否存在同时满足下列两条件的直线l:(1)l与抛物线y2=8x有两个不同的交点A和B;
(2)线段AB被直线l1:x+5y-5=0垂直平分.若不存在,说明理由,若存在,求出直线l的方程.
分析 假定存在同时满足下列两条件的直线l.设在抛物线y2=8x上两点A(x1,y1),B(x2,y2),运用点差法求得AB的斜率,再由两直线垂直的条件和中点坐标公式计算可得中点坐标,进而得到所求直线方程.
解答 解:假定存在同时满足下列两条件的直线l.
设在抛物线y2=8x上两点A(x1,y1),B(x2,y2),
则有y12=8x1,y22=8x2,
相减可得(y1-y2)(y1+y2)=8(x1-x2),
可得kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{8}{{y}_{1}+{y}_{2}}$,
∵线段AB被直线l1:x+5y-5=0垂直平分,
由于${k}_{{l}_{1}}$=-$\frac{1}{5}$,则kAB=5,
即$\frac{8}{{y}_{1}+{y}_{2}}$=5,即有y1+y2=$\frac{8}{5}$,
设线段AB的中点为M(x0,y0).
则有y0=$\frac{4}{5}$,代入x+5y-5=0得x0=1.于是AB中点为M(1,$\frac{4}{5}$).
故存在符合题设条件的直线,其方程为:
y-$\frac{4}{5}$=5(x-1)即25x-5y-21=0.
点评 本题考查抛物线的方程和性质,主要考查抛物线方程的运用,同时考查两直线垂直的条件和线段中点坐标公式的运用,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
2.在长方体ABCD-A1B1C1D1的八个顶点任两点连线中,随机取一直线,则该直线与平面AB1D1平行的概率为( )
| A. | $\frac{3}{14}$ | B. | $\frac{5}{14}$ | C. | $\frac{3}{28}$ | D. | $\frac{5}{28}$ |
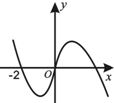
 已知函数f(x)的导函数f′(x)的图象如图所示,那么函数f(x)的图象最有可能的是图中的( )
已知函数f(x)的导函数f′(x)的图象如图所示,那么函数f(x)的图象最有可能的是图中的( )


 如图,一条直线上有三点A,B,C,点C在点A与点B之间,点P是此直线外一点,设∠APC=α,∠BPC=β.求证:$\frac{sin(α+β)}{PC}=\frac{sinα}{PB}+\frac{sinβ}{PA}$.
如图,一条直线上有三点A,B,C,点C在点A与点B之间,点P是此直线外一点,设∠APC=α,∠BPC=β.求证:$\frac{sin(α+β)}{PC}=\frac{sinα}{PB}+\frac{sinβ}{PA}$. 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC=BC,AB=2A1A=4.以AB,BC为邻边作平行四边形ABCD,连接A1D和DC1.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AC=BC,AB=2A1A=4.以AB,BC为邻边作平行四边形ABCD,连接A1D和DC1.