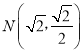题目内容
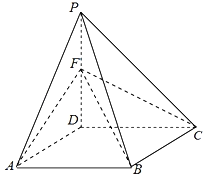
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,其右焦点F到其右准线的距离为1,离心率为
,其右焦点F到其右准线的距离为1,离心率为![]() ,A,B分别为椭圆
,A,B分别为椭圆![]() 的上、下顶点,过点F且不与x轴重合的直线l与椭圆
的上、下顶点,过点F且不与x轴重合的直线l与椭圆![]() 交于C,D两点,与y轴交于点P,直线
交于C,D两点,与y轴交于点P,直线![]() 与
与![]() 交于点Q.
交于点Q.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据题意列出等式:![]() ,
,![]() ,联立即得解;
,联立即得解;
(2)设直线l的方程为![]() ,与椭圆联立,利用弦长公式表示
,与椭圆联立,利用弦长公式表示![]() ,代入求解即可;
,代入求解即可;
(3)设![]() ,
,![]() ,表示
,表示![]() 方程,联立得到
方程,联立得到![]() 的坐标,利用韦达定理化简
的坐标,利用韦达定理化简![]() ,利用坐标表示
,利用坐标表示![]() ,可得证.
,可得证.
(1)解:由题意可知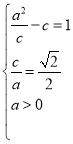 ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,
所以椭圆的标准方程为![]()
(2)解:因为直线l不与x轴重合,所以斜率不为0.
因为l过点![]() ,所以设直线l的方程为
,所以设直线l的方程为![]() .
.
由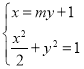 ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
则![]()
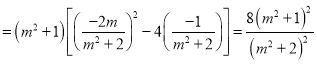
因为![]() ,所以
,所以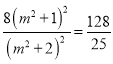 ,得
,得![]() ,所以
,所以![]() ,
,
所以直线l的方程为![]()
(3)证明:在![]() 中令
中令![]() 得
得![]() ,所以
,所以![]() .
.
而直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
由此得到![]()
![]() .
.
不妨设![]() ,则
,则![]() ①,
①,![]() ②,
②,
所以![]() ③.
③.
将①②③代入![]() 式,得
式,得
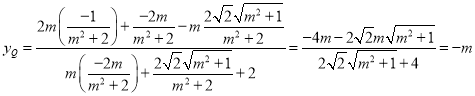 ,
,
所以![]() 为定值
为定值

【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【题目】政府工作报告指出,2019年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2020年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制,某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续5年来的科技投入x(百万元)与收益y(百万元)的数据统计如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)请根据表中数据,建立y关于x的线性回归方程;
(2)按照(1)中模型,已知科技投入8百万元时收益为140百万元,求残差![]() (残差
(残差![]() 真实值-预报值).
真实值-预报值).
参考数据:回归直线方程![]() ,其中
,其中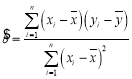 .
.
【题目】质量是企业的生命线,某企业在一个批次产品中随机抽检![]() 件,并按质量指标值进行统计分析,得到表格如表:
件,并按质量指标值进行统计分析,得到表格如表:
质量指标值 | 等级 | 频数 | 频率 |
| 三等品 | 10 | 0.1 |
| 二等品 | 30 |
|
| 一等品 |
| 0.4 |
| 特等品 | 20 | 0.2 |
合计 |
| 1 | |
(1)求![]() ,
,![]() ,
,![]() ;
;
(2)从质量指标值在![]() 的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.
的产品中,按照等级分层抽样抽取6件,再从这6件中随机抽取2件,求至少有1件特等品被抽到的概率.