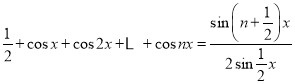题目内容
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点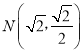 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
【答案】(1)![]() ,
, ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据椭圆的定义可知曲线C是以两定点F1,F2为焦点,长半轴长为2的椭圆,再代入点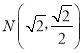 求得椭圆中的基本量即可.
求得椭圆中的基本量即可.
(2)设直线![]() ,再联立椭圆的方程,得出韦达定理,代入
,再联立椭圆的方程,得出韦达定理,代入![]() 进行计算可得
进行计算可得![]() 证明即可.
证明即可.
(1)解:设M(x,y),因为|MF1|+|MF2|=4>2m,所以曲线C是以两定点F1,F2为焦点,长半轴长为2的椭圆,所以a=2.
设椭圆C的方程为![]() 1(b>0),代入点
1(b>0),代入点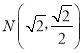 得b2=1,
得b2=1,
由c2=a2﹣b2,得c2=3,
所以![]() ,故曲线C的方程为
,故曲线C的方程为![]() ;
;
(2)证明:设直线l:x=ty![]() ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),
椭圆的右顶点为P(2,0),联立方程组
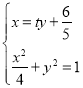 消去x得
消去x得![]() 0.
0.
△>0,y1+y2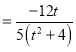 ,y1y2
,y1y2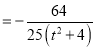 ,
,
所以![]()
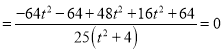 ,∴
,∴![]() ,
,
故点P在以AB为直径的圆上,即以AB为直径的圆过曲线C的右顶点.

练习册系列答案
相关题目