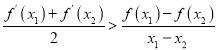题目内容
【题目】在①![]() ;②
;②![]() ;③
;③![]()
![]() ,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这三个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在△![]() 中,内角A,B,C所对的边分别为
中,内角A,B,C所对的边分别为![]() .且满足_________.
.且满足_________.
(1)求![]() ;
;
(2)已知![]() ,△
,△![]() 的外接圆半径为
的外接圆半径为![]() ,求△
,求△![]() 的边AB上的高
的边AB上的高![]() .
.
【答案】答案不唯一,具体见解析
【解析】
选择条件①:(1)利用正弦定理将边化角,再利用![]() 化简,及可求出
化简,及可求出![]() ,即可得出
,即可得出![]() 的值.
的值.
(2)利用正弦定理结合外接圆半径![]() 与
与![]() 的值求出
的值求出![]() ,代入角
,代入角![]() 的余弦定理结合
的余弦定理结合![]() ,可得到
,可得到![]() ,再利用等面积法:
,再利用等面积法: ![]() ,即可求出答案.
,即可求出答案.
选择条件②:(1)利用正弦定理将边化角,再利用![]() 化简,及可求出
化简,及可求出![]() ,即可得出
,即可得出![]() 的值.
的值.
(2)利用正弦定理结合外接圆半径![]() 与
与![]() 的值求出
的值求出![]() ,代入角
,代入角![]() 的余弦定理结合
的余弦定理结合![]() ,可得到
,可得到![]() ,再利用等面积法:
,再利用等面积法: ![]() ,即可求出答案.
,即可求出答案.
选择条件③:(1)利用正弦定理将边化角,再利用![]() 化简,及可求出
化简,及可求出![]() ,即可得出
,即可得出![]() 的值.
的值.
(2)利用正弦定理结合外接圆半径![]() 与
与![]() 的值求出
的值求出![]() ,代入角
,代入角![]() 的余弦定理结合
的余弦定理结合![]() ,可得到
,可得到![]() ,再利用等面积法:
,再利用等面积法: ![]() ,即可求出答案.
,即可求出答案.
选择条件①:
(1)因为![]() ,
,
所以由正弦定理得![]() ,
,
即![]() ,
,
故![]() .
.
又![]() ,
,
所以![]() .
.
由![]()
![]()
所以![]() .
.
(2)由正弦定理得![]() ,
,
由余弦定理得![]() ,
,
所以![]() .
.
于是得![]() 的面积
的面积![]() ,
,
所以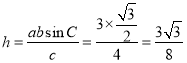 .
.
选择条件②:
(1)因为![]() ,
,
由正弦定理得![]() ,
,
即![]() ,
,
于是![]() .
.
在![]() ,
,
所以![]() ,
,
![]() .
.
(2)由正弦定理得![]() ,
,
由余弦定理得![]()
![]() ,
,
所以![]() ,
,
于是得![]() 的面积
的面积![]() ,
,
所以![]() .
.
选择条件③:
(1)因为![]() ,
,
所以由正弦定理得![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() ,
,
所以![]() .
.
(2)由正弦定理得![]() ,
,
由余弦定理得![]() ,
,
所以![]() .
.
于是得![]() 的面积
的面积![]() ,
,
所以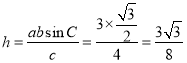 .
.

练习册系列答案
相关题目