Question

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠DAB＝60°，AD⊥PD，点F为棱PD的中点．

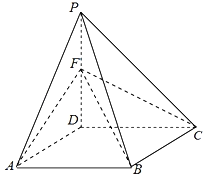
（1）在棱BC上是否存在一点E，使得CF∥平面PAE，并说明理由；

（2）若AC⊥PB，二面角D﹣FC﹣B的余弦值为时，求直线AF与平面BCF所成的角的正弦值．

Answer 1

【答案】（1）存在，见解析（2）．

【解析】

（1）取点E为棱BC的中点，取PA的中点Q，连结EQ、FQ，利用已知结合三角形中位线定理可证四边形CEQF为平行四边形，得到CF∥EQ，再由直线与平面平行的判定得CF∥平面PAE；

（2）取AB中点M，以D为坐标原点，分别以DM，DC，DP所在直线为x，y，z轴建立空间直角坐标系.设FD＝a，利用平面FBC与平面DFC的所成角的余弦值求得a，可得平面BCF的一个法向量及的坐标再由两向量所成角的余弦值可得FA与平面BCF所成的角的正弦值.

（1）在棱BC上存在点E，使得CF∥平面PAE，点E为棱BC的中点.

证明：取PA的中点Q，连结EQ、FQ，

由题意，FQ∥AD且，CE∥AD且，

故CE∥FQ且CE＝FQ.

∴四边形CEQF为平行四边形.

∴CF∥EQ，又平面PAE，在平面PAE内，

∴CF∥平面PAE；

（2）取AB中点M，

以D为坐标原点，分别以DM，DC，DP所在直线为x，y，z轴建立空间直角坐标系.

设FD＝a，则D（0，0，0），F（0，0，a），C（0，2，0），

B（，1，0），A（）.

，.

设平面FBC的一个法向量为.

由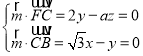，取x＝1，得；

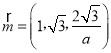取平面DFC的一个法向量为.

由题意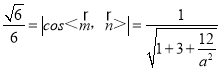，，解得a.

∴.

设直线AF与平面BCF所成的角为θ，

则.

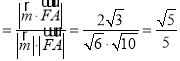即直线AF与平面BCF所成的角的正弦值为.