题目内容
【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若函数![]() ,
, ![]() 是函数
是函数![]() 的两个零点,
的两个零点, ![]() 是函数
是函数![]() 的导函数,证明:
的导函数,证明: ![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)先求函数导数,根据导函数是否变号进行讨论,当![]() 时,
时, ![]() ,
, ![]() 递增,当
递增,当![]() 时,导函数有一零点,导函数先正后负,故得增区间为
时,导函数有一零点,导函数先正后负,故得增区间为![]() ,减区间为
,减区间为![]() ;(2)利用分析法先等价转化所证不等式:要证明
;(2)利用分析法先等价转化所证不等式:要证明![]() ,只需证明
,只需证明![]()
![]() ,即证明
,即证明![]() ,即证明
,即证明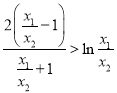 ,再令
,再令![]() ,构造函数
,构造函数![]() ,利用导数研究函数
,利用导数研究函数![]() 单调性,确定其最值:
单调性,确定其最值: ![]() 在
在![]() 上递增,所以
上递增,所以![]() ,即可证得结论.
,即可证得结论.
试题解析:(1) ![]() 的定义域为
的定义域为![]() ,
, ![]()
当![]() 时,
时, ![]() ,
, ![]() 递增
递增
当![]() 时,
时, ![]()
![]() 递增;
递增; ![]() 递减
递减
综上:∴当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]()
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]()
(2)由![]() 是函数
是函数![]() 的两个零点有
的两个零点有![]()
![]() ,相减得
,相减得![]()
又∵![]()
∴![]()
所以要证明![]() ,只需证明
,只需证明![]()
![]()
即证明![]() ,即证明
,即证明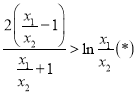
令![]() ,则
,则![]()
则![]() ,
, ![]()
∴![]() 在
在![]() 上递减,
上递减, ![]() ,∴
,∴![]() 在
在![]() 上递增,
上递增, ![]()
所以![]() 成立,即
成立,即![]()

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:
| A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料,求出此最大利润.