题目内容
【题目】已知函数
.
(1)求
的单调区间；
(2)若函数
， 
是函数
的两个零点， 
是函数
的导函数，证明： 
.
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）先求函数导数，根据导函数是否变号进行讨论，当
时， 
， 
递增，当
时，导函数有一零点，导函数先正后负，故得增区间为
，减区间为
；（2）利用分析法先等价转化所证不等式：要证明
，只需证明
，即证明
，即证明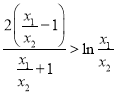
，再令
，构造函数
，利用导数研究函数
单调性，确定其最值： 
在
上递增，所以
，即可证得结论.
试题解析：(1) 
的定义域为
， 
当
时， 
， 
递增
当
时， 
递增；
递减
综上：∴当
时， 
的单调增区间为
，单调减区间为
当
时， 
的单调增区间为
（2）由
是函数
的两个零点有
，相减得
又∵
∴
所以要证明
，只需证明
即证明
，即证明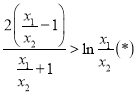
令
，则
则
， 
∴
在
上递减， 
，∴
在
上递增， 
所以
成立，即
练习册系列答案
相关题目
【题目】某市对贫困家庭自主创业给予小额贷款补贴，每户贷款额为
万元，贷款期限有
个月、
个月、
个月、
个月、
个月五种，这五种贷款期限政府分别需要补助
元、
元、
元、
元、
元，从
年享受此项政策的困难户中抽取了
户进行了调查统计，选取贷款期限的频数如下表：
贷款期限 |
|
|
|
|
|
频数 |
|
|
|
|
|
以商标各种贷款期限的频率作为
年贫困家庭选择各种贷款期限的概率.
（1）某小区
年共有
户准备享受此项政策，计算其中恰有两户选择贷款期限为
个月的概率；
（2）设给享受此项政策的某困难户补贴为
元，写出
的分布列，若预计
年全市有
万户享受此项政策，估计
年该市共要补贴多少万元.
