题目内容
(本题满分14分)
已知函数 且存在
且存在 使
使
(I)证明: 是R上的单调增函数;
是R上的单调增函数;
(II)设 其中
其中 
证明:
(III)证明:
已知函数
 且存在
且存在 使
使
(I)证明:
 是R上的单调增函数;
是R上的单调增函数;(II)设
 其中
其中 
证明:

(III)证明:

(I)∵
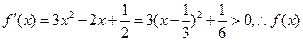 是R上的单调增函数.
是R上的单调增函数.(II)∵
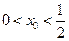 , 即
, 即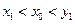 .又
.又 是增函数, ∴
是增函数, ∴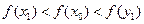 .
.即
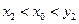 .又
.又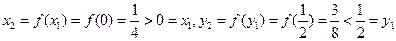 ,
,综上,
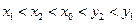 .用数学归纳法证明如下:
.用数学归纳法证明如下:(1)当n=1时,上面已证明成立.
(2)假设当n=k(k≥1)时有
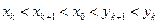 .
.当n=k+1时,由
 是单调增函数,有
是单调增函数,有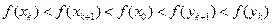 ,
,∴
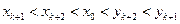
由(1)(2)知对一切n=1,2,…,都有
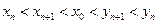 .
.(III)
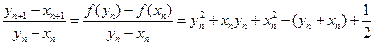
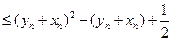
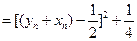 .
.由(Ⅱ)知
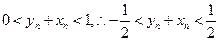
∴
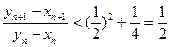
略

练习册系列答案
相关题目
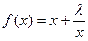 ,常数
,常数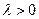 .
.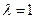 ,判断
,判断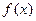 在区间
在区间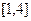 上的单调性,并加以证明;
上的单调性,并加以证明;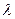 的取值范围.
的取值范围.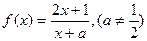 ,
,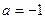 ,证明
,证明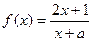 在区间
在区间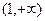 上是增函数;
上是增函数;
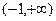 上是单调函数,试求实数
上是单调函数,试求实数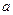 的取值范围。
的取值范围。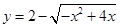 的值域是( )
的值域是( )



 是(-∞,+∞)上的减函数,那么a的取值范围是
是(-∞,+∞)上的减函数,那么a的取值范围是 )
)  ,
, 的值域是
的值域是 ,+
,+ )
) ,1)
,1)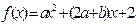 (其中
(其中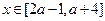 )是偶函数, 则实数
)是偶函数, 则实数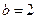 ;
;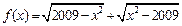 既是奇函数又是偶函数;
既是奇函数又是偶函数;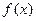 是定义在
是定义在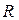 上的奇函数,若当
上的奇函数,若当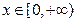 时,
时, 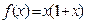 ,则当
,则当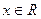 时,
时, 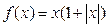 ;
;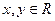 都满足
都满足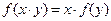
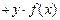 , 则
, 则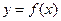 是定义在
是定义在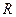 上的增函数,函数
上的增函数,函数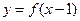 的图象关于点
的图象关于点 (1 , 0)对称,若对任意的
(1 , 0)对称,若对任意的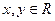 ,不等式
,不等式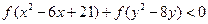 恒成立,则当
恒成立,则当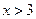 时,
时,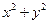 的取值范围是____▲_____
的取值范围是____▲_____ ,有下列命题:
,有下列命题: 轴对称;
轴对称; 时,
时, 是增函数;当
是增函数;当 时,
时, ;
; 在区间(-1,0)、(2,+∞)上是增函数;
在区间(-1,0)、(2,+∞)上是增函数;