题目内容
10. 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别是棱DD1、D1C1的中点,则直线OM( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,M、N分别是棱DD1、D1C1的中点,则直线OM( )| A. | 与AC、MN均垂直相交 | B. | 与AC垂直、与MN不垂直 | ||
| C. | 与MN垂直,与AC不垂直 | D. | 与AC、MN均不垂直 |
分析 此题的条件使得建立空间坐标系方便,且选项中研究的位置关系也适合用空间向量来证明其垂直关系,故应先建立坐标系,设出边长,据几何特征,给出各点的坐标,验证向量内积是否为零
解答 解:以DA、DC、DD1所在的直线为x轴、y轴、z轴建立空间直角坐标系.如图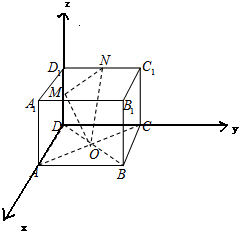
因为正方体的棱长为2,
则D(0,0,0)、D1(0,0,2)、M(0,0,1)、A(2,0,0)、C(0,2,0)、O(1,1,0)、N(0,1,2).
∴$\overrightarrow{OM}$=(-1,-1,1),$\overrightarrow{MN}$=(0,1,1),$\overrightarrow{AC}$=(-2,2,0).
∴$\overrightarrow{OM}•\overrightarrow{AC}$=0,$\overrightarrow{OM}•\overrightarrow{MN}$=0,
∴OM⊥AC,OM⊥MN.
故选A.
点评 本题考查用空间向量的方法来判断线线垂直,解答本题的关键是正确建立坐标系,使所求坐标化,利用向量的坐标运算解答.

练习册系列答案
相关题目
20.复数$\frac{(1-i)(1+i)}{i}$在复平面中所对应的点到原点的距离是( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
5.若二项式(x2-$\frac{2}{x}$)n 的展开式中的二项式系数和为64,则展开式中的常数项为( )
| A. | -240 | B. | -160 | C. | 160 | D. | 240 |
15.函数y=x2-1(x≤0)的反函数是( )
| A. | y=$\sqrt{x+1}$(x≥-1) | B. | y=±$\sqrt{x+1}$(x≥-1) | C. | y=-$\sqrt{x+1}$(x≥-1) | D. | y=-$\sqrt{-x+1}$(x≤1) |
2.甲乙两人下棋,和棋的概率是$\frac{1}{2}$,乙获胜的概率是$\frac{1}{3}$,则甲不输的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
20.设向量$\overrightarrow{a}$=(m,2)(m≠0),$\overrightarrow{b}$=(n,-1),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\frac{n}{m}$=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |